Question

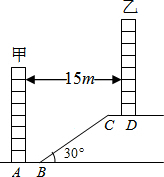（2010•本溪一模）某住宅小区为了美化环境，增加绿地面积，决定在甲楼和乙楼之间的坡地上建一块斜坡草地为绿化带，如图，已知两楼的水平距离为15米，距离甲楼4米（即AB=4米）开始修建坡角为30°的斜坡，斜坡的顶端距离乙楼2米（即CD=2米），如果绿化带总长为10米，求绿化带的面积．（

3

≈1.732，结果保留整数）

Answer 1

分析：作CE⊥AB于点E，即可求得BE的长度，在直角△BCE中，利用三角函数即可求得BC的长，即可求得绿化带的宽度，然后乘以长，即可得到面积．

解答：解：作CE⊥AB于点E，则BE=15-AB-CD=15-4-2=9（米），
∵在直角△BEC中，cos∠CBE=

BE

BC

，
∴BC=

BE

cos∠CBE

=

9

3 2

=6

3

（米）．
则绿化地的面积是：6

3

×10=60

3

≈104（米²）．
答：绿化地的面积是104m²．

点评：本题考查了三角函数的计算，正确作出辅助线，求得BC的长度是关键．