题目内容
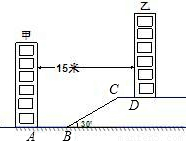
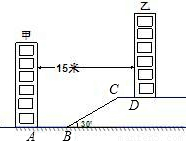
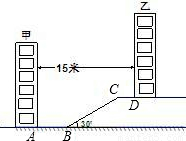
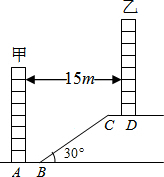
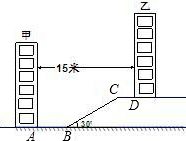某住宅小区为了美化环境，增加绿地面积，决定在坡地上的甲楼和乙楼之间建一块斜坡草地，如图，已知两楼的水平距离为15米，距离甲楼2米（即AB=2米）开始修建坡角为30°的斜坡，斜坡的顶端距离乙楼4米（即CD=4米），求斜坡BC的长度（结果保留根号）．
分析：本题可通过构建直角三角形来求解．如果过C作CE⊥AB于E，那么BE=15-AB-CD=9，直角三角形CBE中，有了∠CBE的度数，有了BE的长度，那么BC便可求出来了．
解答：
解：过点C作CE⊥地面于点E
∵两楼水平距离为15米，
且AB=2米，CD=4米
∴BE=15-2-4=9米
在Rt△BCE中，cos30°=
BC=BE•
=9•
=6
（米）
答：斜坡BC的长度为6
米．
解：过点C作CE⊥地面于点E∵两楼水平距离为15米，
且AB=2米，CD=4米
∴BE=15-2-4=9米
在Rt△BCE中，cos30°=
| BE |
| BC |
BC=BE•
| 1 |
| cos30° |
=9•
| 2 | ||
|
=6
| 3 |
答：斜坡BC的长度为6
| 3 |
点评：可通过作辅助线构造直角三角形，再把条件和问题转化到这个直角三角形中，使问题解决．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
（2010•本溪一模）某住宅小区为了美化环境，增加绿地面积，决定在甲楼和乙楼之间的坡地上建一块斜坡草地为绿化带，如图，已知两楼的水平距离为15米，距离甲楼4米（即AB=4米）开始修建坡角为30°的斜坡，斜坡的顶端距离乙楼2米（即CD=2米），如果绿化带总长为10米，求绿化带的面积．（
