题目内容
已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1,x2(x1<x2),则对于下列结论:
①当x=-2时,y=1;
②方程kx2+(2k-1)x-1=0有两个不相等的实数根x1,x2;
③x2-x1=
.
其中正确的结论有 (只需填写序号即可).
①当x=-2时,y=1;
②方程kx2+(2k-1)x-1=0有两个不相等的实数根x1,x2;
③x2-x1=
| ||
| k |
其中正确的结论有
考点:抛物线与x轴的交点
专题:推理填空题
分析:直接根据抛物线与x轴的交点问题、根与系数的关系对各小题进行逐一分析即可.
解答:解:①当x=-2时,y=4k-2×(2k-1)-1=4k-4k+2-1=1,故本小题正确;
②∵抛物线x轴交点的横坐标为x1、x2(x1<x2),
∴方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2,故本小题正确;
③∵二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1、x2(x1<x2),
∴x1+x2=
,x1•x2=-
∴x2-x1=
=
=
=
,故本小题错误,
故答案为:①②.
②∵抛物线x轴交点的横坐标为x1、x2(x1<x2),
∴方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2,故本小题正确;
③∵二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1、x2(x1<x2),
∴x1+x2=
| 1-2k |
| k |
| 1 |
| k |
∴x2-x1=
| (x2+x1)2-4x1x2 |
(
|
|
| ||
| |k| |
故答案为:①②.
点评:本题考查的是抛物线与x轴的交点问题,熟知二次函数与一元二次方程的关系、一元二次方程根与系数的关系是解答此题的关键.

练习册系列答案
相关题目
下列各式计算正确的是( )
| A、a+2a=3a2 |
| B、(-a3)2=a6 |
| C、a3•a2=a6 |
| D、(a+b)2=a2+b2 |

 如图,在菱形ABCD中,AB=2,∠A=60°.则菱形ABCD的面积S=
如图,在菱形ABCD中,AB=2,∠A=60°.则菱形ABCD的面积S= 如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,若OE=2,则菱形ABCD的周长是
如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,若OE=2,则菱形ABCD的周长是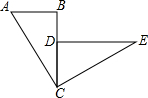 如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是
如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是