题目内容
20.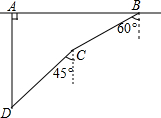 近年来,我国南海诸岛不断受到外国非法骚扰,为此,我军经常会做针对性海上演习,如图,在一次军事演习中,蓝方在一条东西轴向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
近年来,我国南海诸岛不断受到外国非法骚扰,为此,我军经常会做针对性海上演习,如图,在一次军事演习中,蓝方在一条东西轴向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
分析 过点C作CE⊥AB于点E,CF⊥AD于点F,根据已知条件求出CE和CF,再根据四边形AFCE是矩形,得出AF=CE,最后根据AD=AF+FD=CE+FD,即可得出答案.
解答  解:过点C作CE⊥AB于点E,CF⊥AD于点F,
解:过点C作CE⊥AB于点E,CF⊥AD于点F,
由题意得:∠ABC=30°,∠FCD=45°,CD=CB=1000,
在Rt△BCE中,CE=$\frac{1}{2}$BC=$\frac{1}{2}$×1000=500(米),
在Rt△DCF中,DF=$\frac{\sqrt{2}}{2}$×1000=500$\sqrt{2}$(米),
∵四边形AFCE是矩形,
∴AF=CE,
∴AD=AF+FD=CE+FD=(500+500$\sqrt{2}$)米,
∴拦截点D处到公路的距离是(500+500$\sqrt{2}$)米.
点评 此题考查了解直角三角形的应用,用到的知识点是方向角、在直角三角形中,30°所对的直角边等于斜边的一半、矩形的性质,关键是根据题意求出FD和CE的长.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
10.一条开口向下的抛物线的顶点坐标是(2,3),则这条抛物线有( )
| A. | 最大值3 | B. | 最小值3 | C. | 最大值2 | D. | 最小值-2 |
 边长相等的等边三角形ABC和等边三角形DEF如图所示摆放,重叠部分的周长为6,等边三角形ABC的边长为3.
边长相等的等边三角形ABC和等边三角形DEF如图所示摆放,重叠部分的周长为6,等边三角形ABC的边长为3.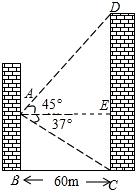 如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)
如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)


