题目内容
将抛物线y=-2x2向左平移2个单位，再向上平移3个单位得到的抛物线，其表达式为（ ）
| A、y=-2（x+2）2+3 |
| B、y=-2（x-2）2-3 |
| C、y=-2（x+2）2-3 |
| D、y=-2（x-2）2+3 |
考点：二次函数图象与几何变换
专题：几何变换
分析：先确定原抛物线的顶点坐标为（0，0），再利用点的平移规律得到点（0，0）向左平移2个单位，再向上平移3个单位得到的对应点的坐标为（-2，3），
然后利用顶点式写出平移后的抛物线解析式．
然后利用顶点式写出平移后的抛物线解析式．
解答：解：抛物线y=-2x2的顶点坐标为（0，0），把点（0，0）向左平移2个单位，再向上平移3个单位得到的对应点的坐标为（-2，3），
所以平移的抛物线解析式为y=2（x+2）2+3．
故选A．
所以平移的抛物线解析式为y=2（x+2）2+3．
故选A．
点评：本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
相关题目
点P（-2，-4）与点Q（6，-4）的位置关系是（ ）
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于直线x=2对称 |
| D、关于直线y=2对称 |
二次函数y=mx2-3x+2m-4的图象过原点，则m=（ ）
| A、m=0 | B、m=2 |
| C、m=-2 | D、m=0且m=2 |
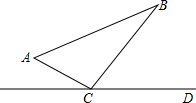如图，△ABC中，∠ACB=90°，AC=6BC=8．点P从点出发沿A-C-B路径向终点运动，终点为B点；点Q从B点出发沿B-C-A路径向终点运动，终点为A点．点P和Q分别以1和3的运动速度同时开始运动，一点到相应的终点停止运动，某时刻，分别过P和Q作PE⊥L于E，QF⊥L于F．问：点P运动多少时间时，△PEC与QFC全等？请说明理由．