题目内容
13.图①为一张三角形ABC纸片,P点在BC上,今将A折至P时,出现折线BD,其中D点在AC上,如图②所示,若△ABC的面积为80,△DBC的面积为50,则BP与PC的长度比为3:2.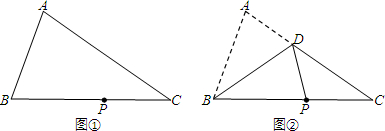
分析 由题意分别计算出△DBP与△DCP的面积,从而BP:PC=S△DBP:S△DCP,问题可解.
解答 解:由题意可得:S△ABD=S△ABC-S△DBC=80-50=30.
由折叠性质可知,S△DBP=S△ABD=30,
∴S△DCP=S△DBC-S△DBP=50-30=20.
∴BP:PC=S△DBP:S△DCP=30:20=3:2.
故答案为:3:2.
点评 本题考查了折叠的性质:折叠前后的两个三角形是全等三角形,它们的面积相等.

练习册系列答案
相关题目
18.下列计算正确的是( )
| A. | a3÷a2=1 | B. | a2+a3=a5 | C. | (a3)2=a5 | D. | a2•a3=a5 |
3. 一个长方体和一个圆柱体按如图所示方式摆放,其主视图是( )
一个长方体和一个圆柱体按如图所示方式摆放,其主视图是( )
 一个长方体和一个圆柱体按如图所示方式摆放,其主视图是( )
一个长方体和一个圆柱体按如图所示方式摆放,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
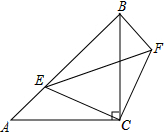 已知:如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.
已知:如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上. 如图,四边形ABCD内接于⊙O,若∠ADC=130°,则∠AOC的大小为100度.
如图,四边形ABCD内接于⊙O,若∠ADC=130°,则∠AOC的大小为100度.