题目内容
12. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F,
如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F,(1)判断△BEO的形状,并说明理由.
(2)若BE=5cm,CF=3cm,求EF的长.
分析 (1)根据角平分线的性质,可得∠EBO=∠CBO,根据平行线的性质,可得∠EOB=∠CBO,根据等腰三角形的判定即可得到结论;
(2)根据角平分线的性质,可得∠EBO与CBO,∠FOC与∠FCO的关系,根据平行线的性质,可得∠EOB与∠CBO,∠FOC与∠BCO的关系,根据等腰三角形的判定,可得BE与EO,CF与FO的关系,根据线段的和差,可得答案.
解答 解:(1)△BEO是等腰三角形,
理由:∵BO平分∠ABC,
∴∠EBO=CBO,
∵EF∥BC,
∴∠EOB=∠CBO,
∴∠EBO=∠EOB,
∴BE=EO,
∴△BEO是等腰三角形;
(2)∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=CBO,∠FOC=∠FCO.
∵EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=EO,CF=FO.
∵EO+OF=EF,
∴EF=BE+CF=8cm.
点评 此题考查了等腰三角形的判定,平行线的性质,利用了等量代换的思想,熟练掌握性质与判定是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.抛物线y=-(x-1)2-2的顶点坐标是( )
| A. | (1,2) | B. | (1,-2) | C. | (-1,2) | D. | (-1,-2) |
17.若x<y成立,则下列不等式一定成立的是( )
| A. | 4x<3y | B. | -x<-y | C. | $\frac{x}{5}$>$\frac{y}{5}$ | D. | x-2015<y-2015 |
2.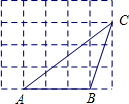 如图,在5×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则sinA的值为( )
如图,在5×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则sinA的值为( )
 如图,在5×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则sinA的值为( )
如图,在5×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则sinA的值为( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |