题目内容
如图，∠AOB=90°，OA=OB=BC=CD．请找出图中的相似三角形，并说明理由．
解：△ABC∽△DAB．
理由如下：设OA=OB=BC=CD=x，
根据勾股定理，AB=
=
x，
AC=
=
x，
AD=
=
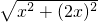x，
∵
=
=
，
=
=，
=
=，
∴==，
∴△ABC∽△DAB．
分析：设OA=OB=BC=CD=x，利用勾股定理表示出AB、AC、AD，再根据三边对应成比例，两三角形相似确定出相似三角形．
点评：本题考查了相似三角形的判定，根据勾股定理求出各边的长，然后求出三边对应成比例是解题的关键．
理由如下：设OA=OB=BC=CD=x，
根据勾股定理，AB=
=x，AC=
=x，AD=
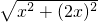=x，∵
==，==，==，∴
==，∴△ABC∽△DAB．
分析：设OA=OB=BC=CD=x，利用勾股定理表示出AB、AC、AD，再根据三边对应成比例，两三角形相似确定出相似三角形．
点评：本题考查了相似三角形的判定，根据勾股定理求出各边的长，然后求出三边对应成比例是解题的关键．
练习册系列答案
相关题目
26、如图，∠AOB=90°，将三角尺的直角顶点落在∠AOB的平分线OC的任意一点P上，使三角尺的两条直角边与∠AOB的两边分别相交于点E、F．
21、如图，∠AOB=90°，点C、D分别在OA、OB上．
（2013•泉州）如图，∠AOB=90°，∠BOC=30°，则∠AOC=
画图、证明：如图，∠AOB=90°，点C、D分别在OA、OB上．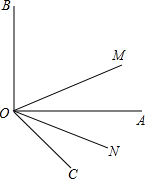
如图，∠AOB=90°，∠AOC为锐角，且ON平分∠AOC，射线OM在∠BON内部．