题目内容
已知正六边形的边长为a，则它的边心距等于分析：经过中心作边的垂线，并连接中心与一个端点构造直角三角形，把正多边形的计算转化为解直角三角形．
解答：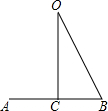
解：经过正六边形的中心O作边AB的垂线OC，
则∠O=30度，
在直角△OBC中，
根据三角函数得到OC=OBcos30°=
a．
解：经过正六边形的中心O作边AB的垂线OC，则∠O=30度，
在直角△OBC中，
根据三角函数得到OC=OBcos30°=
| ||
| 2 |
点评：正多边形的计算一般要经过中心作边的垂线，并连接中心与一个端点构造直角三角形，把正多边形的计算转化为解直角三角形．
练习册系列答案
相关题目
已知正六边形的边长为1cm，分别以它的三个不相邻的顶点为圆心，1cm长为半径画弧（如图），则所得到的三条弧的长度之和为已知正六边形的边长为12cm，则这个正六边形的边心距是（ ）
| A、6cm | ||
| B、12cm | ||
C、6
| ||
D、12
|
已知正六边形的边长为3，则它的外接圆的周长是
已知正六边形的边长为1cm，分别以它的三个不相邻的顶点为圆心，1cm长为半径画弧（如图），则阴影部分面积是