题目内容
18.已知抛物线y=a(x-h)2的对称轴为x=-2,且过点(1,-3).(1)求抛物线的解析式;
(2)画出函数的图象;
(3)从图象上观察,当x取何值时,y随x的增大而增大?当x取何值时,函数有最大值(或最小值)?
分析 (1)首先将对称轴x=-2,(1,-3)代入抛物线y=a(x-h)2中可得a,易得解析式;
(2)根据顶点坐标和点(1,-3)画抛物线;
(3)利用图象回答问题,对称轴的左侧,y随x的增大而增大;因为a是负数,所以函数有最大值.
解答 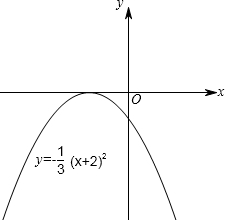 解:(1)∵x=-2为抛物线y=a(x-h)2的对称轴,
解:(1)∵x=-2为抛物线y=a(x-h)2的对称轴,
∴抛物线的解析式为:y=a(x+2)2,
将(1,-3)代入可得,
-3=a(1+2)2,
解得:a=$-\frac{1}{3}$,
∴抛物线的解析式为:y=$-\frac{1}{3}$(x+2)2;
(2)如图所示,
(3)∵该抛物线的对称轴为:x=-2,
∴顶点坐标为(-2,0),
根据抛物线的对称性得,当x<-2时,y随x的增大而增大,
∵-$\frac{1}{3}$<0,
∴函数有最大值,
∴当x=-2时,函数有最大值是0.
点评 本题是二次函数的综合问题,考查了利用待定系数法求二次函数的解析式,并画出抛物线,二次函数的最值问题就是抛物线的顶点问题:(1)当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-$\frac{b}{2a}$时,y最小值=$\frac{4ac-{b}^{2}}{4a}$.(2)当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=-$\frac{b}{2a}$时,y最大值=$\frac{4ac-{b}^{2}}{4a}$.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
8.下列各式中,可分解因式的只有( )
| A. | x2+y2 | B. | x2-y3 | C. | ma+nb | D. | -x2+y2 |
13.抛物线y=ax2+bx+c(a≠0)经过点(-1,1),(3,-3),则方程ax2+(b+1)x+c=0(a≠0)的两根是( )
| A. | x1=-1、x2=3 | B. | x1=-1、x2=-3 | C. | x1=1、x2=3 | D. | x1=1、x2=-3 |
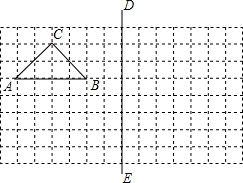 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)