题目内容
3.三角形的两边长分别为2,7,要使这个三角形是直角三角形,则第三条边长是( )| A. | $\sqrt{53}$ | B. | 3$\sqrt{5}$ | C. | $\sqrt{53}$或3$\sqrt{5}$ | D. | $\sqrt{47}$或3$\sqrt{5}$ |
分析 根据勾股定理的逆定理,可设第三条边长为x,如果满足22+72=x2或22+x2=72,即为直角三角形,解出x的值即可解答.
解答 解:设第三条边长为x,
∵三角形是直角三角形,
∴可得,22+72=x2或22+x2=72,
解得x=$\sqrt{53}$或x=3$\sqrt{5}$.
故选C.
点评 本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
18.弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表:
(1)如表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出y与x之间的关系式;
(3)当所挂物体的质量为11.5kg时,求弹簧的长度.
| 所挂物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 弹簧的长度y(cm) | 15 | 15.6 | 16.2 | 16.8 | 17.4 | 18 | 18.6 |
(2)写出y与x之间的关系式;
(3)当所挂物体的质量为11.5kg时,求弹簧的长度.
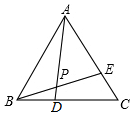 如图,△ABC是等边三角形,点D、E分别是BC、AC边上的两点,其中BD=CE,连接AD、BE交于点P
如图,△ABC是等边三角形,点D、E分别是BC、AC边上的两点,其中BD=CE,连接AD、BE交于点P 已知在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长.
已知在△ABC中,AC=8,∠A=30°,∠B=45°,求AB和BC的长. 如图所示,由三角形ABC平移得到的三角形有5个.
如图所示,由三角形ABC平移得到的三角形有5个.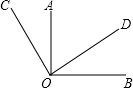 如图,已知OA⊥OB,OC⊥OD,垂足均为点O.求∠BOC+∠AOD的值.
如图,已知OA⊥OB,OC⊥OD,垂足均为点O.求∠BOC+∠AOD的值.