题目内容
如图①,②,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,P是x轴上的一动点,连接CP.
(1)求∠OAC的度数;
(2)p点在x轴上运动,当p点在x轴的负半轴上,且PO=4时,连结CP,请试猜想PC与⊙D的位置关系,并说明理由.
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,△OCQ是等腰三角形?

解:(1)∵∠AOC=60°,AO=AC,
△AOC是等边三角形,
∴∠OAC=60°. …………………………………………3分
(2)∵CP与⊙A相切,…………………………………………4分
证明略 …………………………………………7分
 |
(3)①过点C作CP1⊥OB,垂足为P1,延长CP1交⊙A于Q1;
∵OA是半径,
∴弧OC=弧OQ1
∴OC=OQ1,
∴△OCQ1是等腰三角形;
又∵△AOC是等边三角形,
∴P1O=![]() OA=2 ………………………………………………9分
OA=2 ………………………………………………9分
②过A作AD⊥OC,垂足为D,延长DA交⊙A于Q2,CQ2与x轴交于P2;
∵A是圆心,
∴DQ2是OC的垂直平分线,
∴CQ2=OQ2,
∴△OCQ2是等腰三角形;
过点Q2作Q2E⊥x轴于E,
在Rt△AQ2E中,
∵∠Q2AE=∠OAD=![]() ∠OAC=30°,
∠OAC=30°,
∴Q2E=![]() AQ2=2,AE=2
AQ2=2,AE=2![]() ,
,
∴点Q2的坐标(4+2![]() ,-2) ……………………………………11分
,-2) ……………………………………11分
在Rt△COP1中,
∵P1O=2,∠AOC=60°,
∴CP1=2,
∴C点坐标(2,2![]() );
);
设直线CQ2的关系式为y=kx+b,则
解得
∴y=-x+2+2![]()
当y=0时,x=2+2![]()
∴P2O=2+2![]() ……………………………………14分
……………………………………14分

练习册系列答案
相关题目
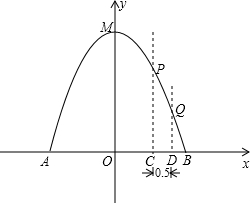 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系. 水柱在与池中心的水平距离为1m处达到最高,高度为3m.
水柱在与池中心的水平距离为1m处达到最高,高度为3m.




