题目内容
解方程
(1)2x(x-3)=5(x-3)
(2)y2+10y+2=0.
解:(1)2x(x-3)=5(x-3),
移项得:2x(x-3)-5(x-3)=0,
∴(x-3)(2x-5)=0,
∴x-3=0或2x-5=0,
∴x1=3,x2=2.5;
(2)y2+10y+2=0,
配方得:(x+5)2=25-2,
∴(x+5)2=23,
∴x=-5±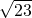 ,
,
x1=-5+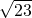 ,x2=-5-
,x2=-5-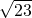 .
.
分析:(1)首先移项,再提取公因式,然后利用两式相乘值为0,这两式中至少有一式值为0即可得出答案;
(2)利用配方法,首先将常数项移项,再方程两边加一次项系数一半的平方,配方即可,从而得出答案;
点评:此题主要考查了因式分解法和配方法解一元二次方程,只有当方程的一边能够分解成两个一次因式,而另一边是0的时候,才能应用因式分解法解一元二次方程,难度适中.
移项得:2x(x-3)-5(x-3)=0,
∴(x-3)(2x-5)=0,
∴x-3=0或2x-5=0,
∴x1=3,x2=2.5;
(2)y2+10y+2=0,
配方得:(x+5)2=25-2,
∴(x+5)2=23,
∴x=-5±
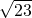 ,
,x1=-5+
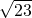 ,x2=-5-
,x2=-5-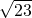 .
.分析:(1)首先移项,再提取公因式,然后利用两式相乘值为0,这两式中至少有一式值为0即可得出答案;
(2)利用配方法,首先将常数项移项,再方程两边加一次项系数一半的平方,配方即可,从而得出答案;
点评:此题主要考查了因式分解法和配方法解一元二次方程,只有当方程的一边能够分解成两个一次因式,而另一边是0的时候,才能应用因式分解法解一元二次方程,难度适中.

练习册系列答案
相关题目