题目内容
 如图,AB是⊙O的弦,∠AOB=120°.若⊙O的半径为20,则△OAB的面积为( )
如图,AB是⊙O的弦,∠AOB=120°.若⊙O的半径为20,则△OAB的面积为( )A、25
| ||
B、50
| ||
C、100
| ||
D、200
|
考点:垂径定理,含30度角的直角三角形,勾股定理
专题:
分析:首先过点O作OD⊥AB于点D,由垂径定理可得AD=
AB,然后由OA=OB,∠AOB=120°,可得∠A=30°,继而求得OD与AB的长,则可求得答案.
| 1 |
| 2 |
解答: 解:过点O作OD⊥AB于点D,
解:过点O作OD⊥AB于点D,
∴AD=
AB,
∵OA=OB,∠AOB=120°,
∴∠A=30°,
∴OD=
OA=
×20=10,
∴AD=
=10
,
∴AB=2AD=20
,
∴S△OAB=
AB•OD=
×20
×10=100
.
故选C.
 解:过点O作OD⊥AB于点D,
解:过点O作OD⊥AB于点D,∴AD=
| 1 |
| 2 |
∵OA=OB,∠AOB=120°,
∴∠A=30°,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| OA2-OD2 |
| 3 |
∴AB=2AD=20
| 3 |
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故选C.
点评:此题考查了垂径定理、含30°角的直角三角形的性质以及勾股定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做下去,…则△AnAn+1B的面积为( )
如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做下去,…则△AnAn+1B的面积为( )A、8×(
| ||
B、4×(
| ||
C、8×(
| ||
D、8×(
|
点A(-2,-3)和点B(2,3)在直角坐标系中( )
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、不关于坐标轴和原点对称 |
下列说法不正确的有( )
①最大的负整数是-1;②相反数是本身的数是正数;③有理数分为正有理数和负有理数;④在数轴上表示-a的点一定在原点的左边;⑤在数轴上-7与-9之间的有理数是-8.
①最大的负整数是-1;②相反数是本身的数是正数;③有理数分为正有理数和负有理数;④在数轴上表示-a的点一定在原点的左边;⑤在数轴上-7与-9之间的有理数是-8.
| A、2个 | B、3个 | C、4个 | D、5个 |
在平面直角坐标系中,某个图形经过了一定的变化,大小和形状都没有改变,这个图形上各点的坐标有可能做了一种变化,下列变化中,正确的是( )
| A、纵、横坐标分别乘以2 | ||
B、纵、横坐标分别变成原来的
| ||
| C、横坐标不变,纵坐标分别加2 | ||
| D、纵坐标不变,横坐标分别变成原来的2倍 |
要使a+8的值与2-a的值相等,则a的值应为( )
| A、5 | B、-5 | C、3 | D、-3 |
若方程组
的解满足kx+(k-3)y=1,则k的值为( )
|
| A、1 | B、2 | C、3 | D、4 |
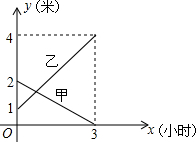 某企业有甲乙两个长方形的蓄水池,将甲池中的水注入乙池,甲乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数图象如图,结合图象回答下列问题:
某企业有甲乙两个长方形的蓄水池,将甲池中的水注入乙池,甲乙两个蓄水池中水的深度y(m)与注水时间x(h)之间的函数图象如图,结合图象回答下列问题: