题目内容
 如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做下去,…则△AnAn+1B的面积为( )
如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做下去,…则△AnAn+1B的面积为( )A、8×(
| ||
B、4×(
| ||
C、8×(
| ||
D、8×(
|
考点:等腰直角三角形
专题:规律型
分析:根据等腰直角三角形的直角边等于斜边的
倍分别表示出A2A3、A3A4、A4A5、A5A6…AnAn+1,再根据等腰直角三角形的面积等于直角边平方的
进行计算即可得解.
| ||
| 2 |
| 1 |
| 2 |
解答:解:由题意可知,截出的直角三角形都是等腰直角三角形,
∴A2A3=
A1A2,
A3A4=
A2A3=(
)2A1A2,
A4A5=
A3A4=(
)3A1A2,
A5A6=
A4A5=(
)4A1A2,
…,
AnAn+1=
An-1An=(
)n-1A1A2,=4×(
)n-1,
所以,△AnAn+1B的面积=
×[4×(
)n-1]2=
×16×
=8×(
)n-1.
故选:C.
∴A2A3=
| ||
| 2 |
A3A4=
| ||
| 2 |
| ||
| 2 |
A4A5=
| ||
| 2 |
| ||
| 2 |
A5A6=
| ||
| 2 |
| ||
| 2 |
…,
AnAn+1=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
所以,△AnAn+1B的面积=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2 |
故选:C.
点评:本题考查了等腰直角三角形的性质,三角形的面积,熟记等腰直角三角形的直角边等于斜边的
倍并表示出AnAn+1的长度是解题的关键.
| ||
| 2 |

练习册系列答案
相关题目
平行四边形具有一般四边形不具有的特征是( )
| A、外角和为360° |
| B、两条对角线 |
| C、不稳定性 |
| D、对角线互相平分 |
射线OE在∠AOB的内部,下列四个式子中,不能判断OE是∠AOB的平分线的是( )
| A、∠AOE=∠EOB | ||
| B、∠AOE+∠EO B=∠AOB | ||
| C、∠AOB=2∠B OE | ||
D、∠AOE=
|
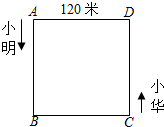 如图,正方形的边长为120米,小明和小华都沿着正方形的边按逆时针方向跑步,二人同时起跑,小明从A点开始,速度是4米/秒,小华从C点开始,速度是5.5米/秒,小华第一次追上小明是在边( )上.
如图,正方形的边长为120米,小明和小华都沿着正方形的边按逆时针方向跑步,二人同时起跑,小明从A点开始,速度是4米/秒,小华从C点开始,速度是5.5米/秒,小华第一次追上小明是在边( )上.| A、AB | B、BC | C、CD | D、DA |
若一次函数y=-3mx-4(m≠0),当x的值增大时,y的值也增大,则m的取值范围为( )
| A、m>0 | B、m<0 |
| C、0<m<3 | D、无法确定 |
 函数图象如图,使y>0相应的x的取值范围是( )
函数图象如图,使y>0相应的x的取值范围是( )| A、x<-3 | B、x>-3 |
| C、x<2 | D、x>2 |
 如图,AB是⊙O的弦,∠AOB=120°.若⊙O的半径为20,则△OAB的面积为( )
如图,AB是⊙O的弦,∠AOB=120°.若⊙O的半径为20,则△OAB的面积为( )A、25
| ||
B、50
| ||
C、100
| ||
D、200
|
 如图是某一立体图形的三种视图,则该立体图形是
如图是某一立体图形的三种视图,则该立体图形是