题目内容
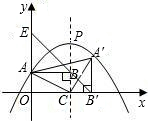
如图在抛物线y=x（a-x）（a＞0）与x轴所围图形的内接矩形ABCD（边BC在x轴上）中，当矩形周长最大时，它的两边长AB=________，BC=________．
2分析：如图，设B（x，0），0＜x＜
，然后根据已知条件可以分别用x表示相等BC、AB的长度，接着就可以用x表示矩形ABCD的周长，最后利用二次函数的性质即可解决问题．解答：
解：如图所示：矩形ABCD中，设B（x，0），0＜x＜
，则C（a-x，0），
则BC=（a-x）-x=a-2x，AB=x（a-x），
∴矩形周长C=2[x（a-x）+（a-2x）]
=-2（x-
）2+
，当x=
时，即BC=a-2×=2，AB=（a-）=
时，周长最大．故答案为：
，2．点评：此题主要考查了抛物线与x轴的交点坐标，解题的关键是利用交点坐标分别表示线段的长度，最后利用二次函数的最值求解．
练习册系列答案
相关题目
如图，抛物线y=-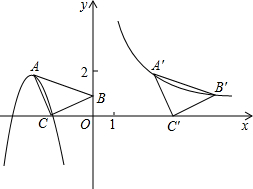
如图，抛物线y=ax2+bx+c的顶点为A（-3，2），与x轴相交于点C（-2，0），过点C画CB⊥AC交y轴于点B，连结AB得△ABC
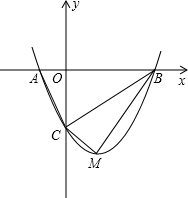如图，抛物线y=mx2-2mx-3m（m＞0）与x轴交于A、B两点，与y轴交于C点，点M为抛物线的顶点．