��Ŀ����
��ͼ��������y=-| 1 |
| 3 |
| 2 |
| 3 |
��1��д����A��P��A������꣨�ú�m��n��ʽ�ӱ�ʾ����
��2����ֱ��BB'��y����E�㣬��֤���߶�B��E��AA�以��ƽ�֣�
��3������A��������������Rt��ABC�����Ϊ1ʱ������������ߵĽ���ʽ���ж��������ߵĶԳ������Ƿ���ڵ�D��ʹ��AA��DΪ���������Σ������ڣ���ֱ��д�����з���������D�����ꣻ�������ڣ���˵�����ɣ�
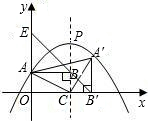
��������1�����������ߵĽ���ʽ�ó�A���P������꣮������ת�����ʿɿ��ó�AB=A��B�䣬BC=B��C�����A��ĺ�����ΪP��ĺ�������A�������ĺͣ���A�����������P��ĺ�������ȣ��ɴ˿ɵó�A������꣮
��2����ֱ��������BCB���У�BC=B��C�����������BCB���ǵ���ֱ�������Σ�����EBA=��BB��C=45�㣬�ɵó�EA=AB=A��B�䣬������֤�����ı���AEA��B����ƽ���ı��Σ���ô����ƽ���ı��ε����ʼ��ɵó���֤��������
��3���ٸ���A�����������ϣ���A���������������ߵĽ���ʽ�пɵó�һ������m��n�ĵ�����ϵ����֪��������ABC�����Ϊ1���ɵó���һ������m��n�ĵ�����ϵ��������ʽ�������m��n��ֵ��Ҳ�������A��A������꣮
�ڱ���ɷ����������
һ��AD=A��D������AD=AA�䣻����AA��=A��D��
�ɸ��ݶԳ��᷽�����D�����꣬Ȼ���������ϵ�������ľ��빫ʽ���е�����ϵ���������D�����꣮
��2����ֱ��������BCB���У�BC=B��C�����������BCB���ǵ���ֱ�������Σ�����EBA=��BB��C=45�㣬�ɵó�EA=AB=A��B�䣬������֤�����ı���AEA��B����ƽ���ı��Σ���ô����ƽ���ı��ε����ʼ��ɵó���֤��������
��3���ٸ���A�����������ϣ���A���������������ߵĽ���ʽ�пɵó�һ������m��n�ĵ�����ϵ����֪��������ABC�����Ϊ1���ɵó���һ������m��n�ĵ�����ϵ��������ʽ�������m��n��ֵ��Ҳ�������A��A������꣮
�ڱ���ɷ����������
һ��AD=A��D������AD=AA�䣻����AA��=A��D��
�ɸ��ݶԳ��᷽�����D�����꣬Ȼ���������ϵ�������ľ��빫ʽ���е�����ϵ���������D�����꣮
�����1���⣺��x=0���õ�y=n��
��A��0��n������m��n��0
��y=-
x2+
mx+n=-
��x-m��2+
m2+n��
��P��m��
m2+n����
��������ã���ABC=��AOC=��OCB=90�㣬
���ı���ABCO�Ǿ��Σ�
��BC=AO=B��C=n��AB=A��B��=OC=m��
��A���������m+n��m����
��2��֤��������EA�䣬AB�䣮
��BC=B��C����BCB��=90�㣬
���EB��O=45�㣮
�ߡ�EOB��=90�㣬
���OEB��=45�㣬
��OB��=OE=m+n��
��AO=n��
��EA=m����A��B��=m��
��A��B��=EA��5�֣�
�ߡ�A��B��C=90�㣬
��EA��A��B�䣮
���ı���AEA��B����ƽ���ı��Σ�
��Խ���B��E��AA�以��ƽ�֣�
��3���⣺�ߵ�A�䣨m+n��m�����������ϣ�
��m=-
��m+n��2+
��m+n��m+n��
�����ã�m-n=
��m+n����m-n��
��m��n����m-n��0��
��m+n=3����n=3-m��
��
AB•BC=1����
mn=1��
��n=3-m����
m•n=1
�ã�
m��3-m��=1��
���
��
������������ȥ��
�������߽���ʽΪy=-
x2+
x+1��
��A'��3��2����A��0��1����
���ۣ��������ߵĶԳ����ϴ��ڵ�D��ʹ��AA��DΪ���������Σ�
��D��������D1��2��1+
����D2��2��1-
����D3��2��5����D4��2��-1����D5��2��0����
��A��0��n������m��n��0
��y=-
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
��P��m��
| 1 |
| 3 |
��������ã���ABC=��AOC=��OCB=90�㣬
���ı���ABCO�Ǿ��Σ�
��BC=AO=B��C=n��AB=A��B��=OC=m��
��A���������m+n��m����
��2��֤��������EA�䣬AB�䣮
��BC=B��C����BCB��=90�㣬
���EB��O=45�㣮
�ߡ�EOB��=90�㣬
���OEB��=45�㣬
��OB��=OE=m+n��
��AO=n��
��EA=m����A��B��=m��
��A��B��=EA��5�֣�
�ߡ�A��B��C=90�㣬
��EA��A��B�䣮
���ı���AEA��B����ƽ���ı��Σ�
��Խ���B��E��AA�以��ƽ�֣�
��3���⣺�ߵ�A�䣨m+n��m�����������ϣ�
��m=-
| 1 |
| 3 |
| 2 |
| 3 |
�����ã�m-n=
| 1 |
| 3 |
��m��n����m-n��0��
��m+n=3����n=3-m��
��
| 1 |
| 2 |
| 1 |
| 2 |
��n=3-m����
| 1 |
| 2 |
�ã�
| 1 |
| 2 |
���
|
|
�������߽���ʽΪy=-
| 1 |
| 3 |
| 4 |
| 3 |
��A'��3��2����A��0��1����
���ۣ��������ߵĶԳ����ϴ��ڵ�D��ʹ��AA��DΪ���������Σ�
��D��������D1��2��1+
| 6 |
| 6 |
����������Ϊ���κ����ۺ��⣬������ͼ�ε���ת�任��ƽ���ı��ε��ж������ʡ����������ε��ж���֪ʶ�㣬�ۺ���ǿ������Ҫ��ϸߣ�����ѧ���������ۣ����ν�ϵ���ѧ˼�뷽����

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������
��ͼ��������y=ax2+bx+c��a��0����x����������A��-1��0����B��3��0��������ͼ��֪y��0ʱ��x��ȡֵ��Χ�ǣ�������| A��-1��x��3 | B��3��x��-1 | C��x��-1��x��3 | D��x��-1��x��3 |
 26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG|
26����֪����ͼ��������C1��C2����x��Գƣ�������C1��C3����y��Գƣ�������C1��C2��C3��x���ཻ��A��B��C��D�ĵ㣻��y�ཻ��E��F���㣻H��G��M�ֱ�Ϊ������C1��C2��C3�Ķ��㣮HN��ֱ��x�ᣬ����ΪN����|OE|��|HN|��|AB|��|HG| ��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4����
��ͼ�������߽�x���ڵ�A��-2��0������B��4��0������y���ڵ�C��0��4���� ��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��PΪԲ�ĵ�Բ������A��������ֱ��BM���У������ڣ������P�����ꣻ�������ڣ���˵�����ɣ� ����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮
����C�ǵ�A���ڵ�B�ĶԳƵ㣬��F���߶�BC���е㣬ֱ��l����F����y��ƽ�У�ֱ��y=-x+m����C����y����D�㣮