题目内容
8. 如图,在△ABC中,CD、AE是△ABC的两条高.
如图,在△ABC中,CD、AE是△ABC的两条高.(1)求证:BD•AB=BE•BC;
(2)连接DE,求证:$\frac{DE}{AC}$=$\frac{BE}{AB}$.
分析 (1)证明△ABE∽△CBD,利用相似三角形的性质可证得结论;
(2)利用(1)的结论可证明△BDE∽△BCA,可证得结论.
解答 证明:
(1)∵CD、AE是△ABC的两条高,
∴∠AEB=∠CDB=90°,且∠ABE=∠CBD,
∴△ABE∽△CBD,
∴$\frac{AB}{BC}$=$\frac{BE}{BD}$,
∴BD•AB=BE•BC;
(2)由(1)可知$\frac{AB}{BC}$=$\frac{BE}{BD}$,
∴$\frac{BE}{AB}$=$\frac{BD}{BC}$,且∠EBD=∠ABC,
∴△BDE∽△BCA,
∴$\frac{DE}{AC}$=$\frac{BE}{AB}$.
点评 本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法(即两边对应成比例,且夹角相等或有两组角对应相等的三角形相似)和相似三角形的性质是解题的关键.

练习册系列答案
相关题目
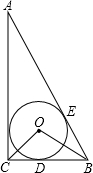 如图,在Rt△ABC中,∠ACB=90°,⊙O是Rt△ABC的内切圆,其半径为1,E是切点,∠BOC=105°,求AE的长.
如图,在Rt△ABC中,∠ACB=90°,⊙O是Rt△ABC的内切圆,其半径为1,E是切点,∠BOC=105°,求AE的长.
 如图,在△ABC中,已知BE⊥AC于点E,则以BE为高的三角形是△ABC,△ABE,△BCE.
如图,在△ABC中,已知BE⊥AC于点E,则以BE为高的三角形是△ABC,△ABE,△BCE.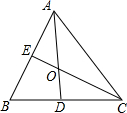 如图,在△ABC中,∠ABC=60°,AD,CE分别平分∠BAC、∠ACB.
如图,在△ABC中,∠ABC=60°,AD,CE分别平分∠BAC、∠ACB.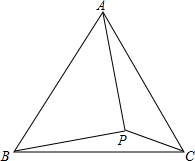 如图,在等边△ABC内有一点P,且PA=2,PB=$\sqrt{3}$,PC=1.
如图,在等边△ABC内有一点P,且PA=2,PB=$\sqrt{3}$,PC=1. 如图,如果AE∥BF,CE∥DF,那么△OAC∽△OBD吗?为什么?
如图,如果AE∥BF,CE∥DF,那么△OAC∽△OBD吗?为什么?