题目内容
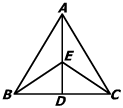
如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
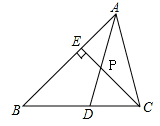

∠ADC=83°,∠APC=123°.
试题分析:在直角三角形BCE中∠BCE=40°,可求出∠B=50°,由三角形内角和可求出∠BCA的度数;由AD是∠BAC的角平分线易求∠ADC的度数,再由CE⊥AB易求∠ACE的度数,从而可求∠APC的度数.
试题解析:∵AD是△ABC的角平分线,∠BAC=66°,
∴∠DAC=∠BAD=33°,
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∠ACB=180°-50°-66°=64°;
∴∠ADC=180°-64°-33°=83°,∠APC=123°
考点: 1.角平分线;2.三角形的内角和.

练习册系列答案
相关题目
 三者之间的关系,并用式子表示出来。
三者之间的关系,并用式子表示出来。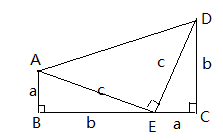
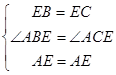
 周长为
周长为 ,点
,点 、
、 都在边
都在边 上,
上, 的平分线垂直于
的平分线垂直于 ,垂足为
,垂足为 ,
, 平分线垂直于
平分线垂直于 ,垂足为
,垂足为 ,若
,若 ,则
,则 的长为( )
的长为( )