题目内容
在△ABC中, AB=AC=2,BD⊥AC,D为垂足,若∠ABD=30°,则BC长为____ _.
2或2 .
.
 .
.试题分析:分为两种情况,画出图形,求出AD、CD的长,根据勾股定理求出BD,再根据勾股定理求出BC即可.
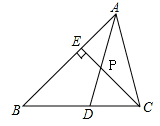
试题解析:分为两种情况:① 如图1,

∵BD⊥AC,
∴∠BDA=90°,
∵∠ABD=30°,AB=2,
∴AD=
 AB=1,
AB=1,∴CD=2-1=1,
由勾股定理得:BD=
 ,
,由勾股定理得:BC=
 ;
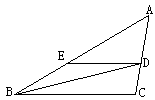
;②如图2,

∵BD⊥AC,
∴∠BDA=90°,
∵∠ABD=30°,AB=2,
∴AD=
 AB=1,∴CD=2+1=3,
AB=1,∴CD=2+1=3,由勾股定理得:BD=
 ,
,由勾股定理得:BC=
 ;
;考点: 1.含30度角的直角三角形;2.等腰三角形的性质;3.勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
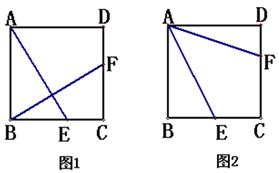
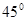 , AE的长为
, AE的长为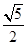 ,试求AF的长度。
,试求AF的长度。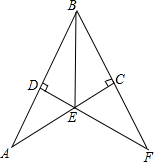
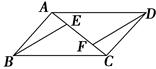
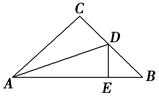
 中,
中, ∥
∥ ,
, :
: =1:2,则△
=1:2,则△ 与四边形
与四边形 的面积之比是( )
的面积之比是( )