Question

4．如图，BC是⊙O的直径，$\widehat{CD}$=$\widehat{DE}$，求证：OD∥BE．（请思考不同证法）

Answer 1

分析 ①连接OE，根据圆心角、弧、弦的关系定理得到∠COD=∠EOD，根据三角形的外角的性质得到∠COD=∠B，根据平行线的判定定理证明即可；
②连接BD，利用与①相似的方法证明．

解答 证明：①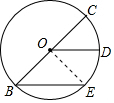连接OE，
∵$\widehat{CD}$=$\widehat{DE}$，
∴∠COD=∠EOD，
∵OB=OE，
∴∠B=∠E，
∵∠COE=∠B+∠E，
∴∠COD=∠B，
∴OD∥BE．
②连接BD，
∵$\widehat{CD}$=$\widehat{DE}$，
∴∠CBD=∠EBD，又∠CBD=∠ODB，
∴∠ODB=∠EBD，
∴OD∥BE．

点评 本题考查的是圆周角定理、圆心角、弧、弦的关系定理，掌握等腰三角形的性质、平行线的判定定理是解题的关键．