题目内容
8.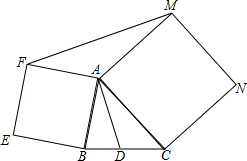 已知:如图,分别以△ABC的边AB、AC为边长向△ABC外作正方形ABEF和正方形ACNM,点D是BC的中点,连接AD、FM.
已知:如图,分别以△ABC的边AB、AC为边长向△ABC外作正方形ABEF和正方形ACNM,点D是BC的中点,连接AD、FM.(1)求证:FM=2AD;
(2)若AB=6,AC=8,∠BAC=60°,求多边形BCNMFE的面积.
分析 在AD的延长线上取点K,使AD=DK,连接BK、CK,则四边形ABDC是平行四边形ABNC,得到CK=AB,∠BAC+∠ACK=180°,根据四边形ABEF、ACNM是正方形,易证AF=AB=CK,AM=AC,∠FAM=∠ACK,根据SAS证明△ACK≌△AMF即可证明FM=AK=2AD.
解答 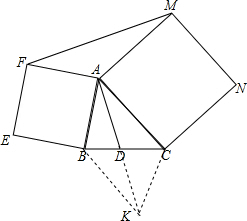 证明:在AD的延长线上取点K,使AD=DK,连接BK、CK,
证明:在AD的延长线上取点K,使AD=DK,连接BK、CK,
∵D是BC的中点,AD=DK,
∴四边形ABKC是平行四边形ABNC,
∴CK=AB,∠BAC+∠ACK=180°,
∵四边形ABEF、ACNM是正方形,
∴AF=AB,AM=AC,∠BAF=∠CAM=90°,
∴AF=CK,∠BAC+∠FAM=360°-∠BAF-∠CAM=180°,
∴∠FAM=∠ACK,
在△ACK和△AMF中,
$\left\{\begin{array}{l}{AF=CK}\\{∠FAM=∠ACK}\\{AM=AC}\end{array}\right.$,
∴△ACK≌△AMF,
∴FM=AK,
∵AK=AD+DK=2AD,
∴FM=2AD.
点评 本题主要考查了全等三角形的判定与性质、正方形的性质以及平行四边形的判定与性质,作辅助线构造全等三角形和平行四边形是解决问题的关键.

练习册系列答案
相关题目
3.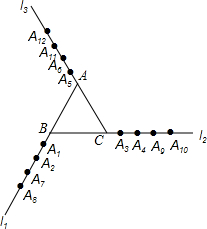 如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
 如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )| A. | 在直线l1上 | B. | 在直线l2上 | ||
| C. | 在直线l3上 | D. | 不能确定在哪条直线上 |
20.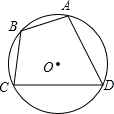 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )| A. | 2π | B. | 4π | C. | 5π | D. | 6π |
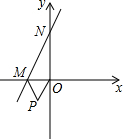 如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.
如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.
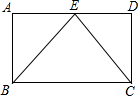 如图所示,在?ABCD中,E为AD的中点,△CBE是等边三角形,求证:?ABCD是矩形.
如图所示,在?ABCD中,E为AD的中点,△CBE是等边三角形,求证:?ABCD是矩形.