题目内容
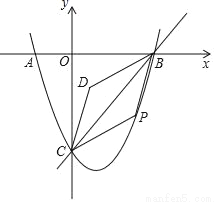
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作?CPBD,设?CPBD的面积为S,点P的横坐标为m.
(1)求抛物线对应的函数表达式;
(2)当点P在第四象限,且?CPBD有两个顶点在x轴上时,求点P的坐标;
(3)求S与m之间的函数关系式;
(4)当x轴将?CPBD的面积分成1:7两部分时,直接写出m的值.
练习册系列答案
相关题目


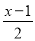 =
=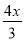 +1; (2)
+1; (2) 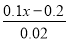 -
-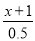 =3.
=3. B.
B.  C.
C.  D.
D. 

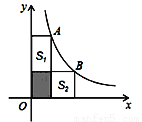
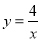 (x>0)的图象上,过点A、B分别向x、y轴作垂线,若阴影部分图形的面积恰好等于S1,则S1+S2=__________.
(x>0)的图象上,过点A、B分别向x、y轴作垂线,若阴影部分图形的面积恰好等于S1,则S1+S2=__________.