Question

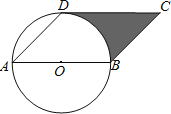
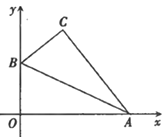
【题目】如图，在平面直角坐标系中，点A,B分别在x,y的正半轴上，以AB所在的直线为对称轴将翻折，使点O落在点C处，若点C的坐标为(4,8)，则 的外接圆半径为_____________ .

Answer 1

【答案】

【解析】

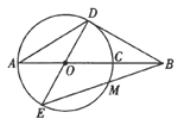
连接OC，过点C作CD⊥y轴于点D，得：CD=4，OD=8，OC=，由∠BOE+∠AOE=90°，∠OAE+∠AOE=90°，得：∠BOE=∠OAE，即：tan∠OAE=tan∠BOE=，得：OA=OE=×=10，作OA的垂直平分线，交OA于点M，交AB于点N，求出AN的值，即可得到答案.

连接OC，过点C作CD⊥y轴于点D，

∵点C的坐标为(4,8)，

∴CD=4，OD=8，OC=，

∵AOB和ACB关于直线AB轴对称，

∴OC⊥AB，OE=CE=，

∵∠BOE+∠AOE=90°，∠OAE+∠AOE=90°，

∴∠BOE=∠OAE，

∴tan∠OAE=tan∠BOE=，

∴OE：AE：OA=1：2：，

∴OA=OE=×=10，

作OA的垂直平分线，交OA于点M，交AB于点N，

∵AB垂直平分OC，

∴点N是 的外接圆的圆心，AN是半径，

∵tan∠OAE=，

∴AN=AM×=×OA×=××10×=.

故答案是：.