题目内容
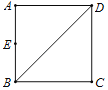
【题目】如图，正方形ABCD的边长为2，点P和点Q分别从点B和点C出发，沿射线BC向右运动，且速度相同，过点Q作QH⊥BD，垂足为H，连接PH，设点P运动的距离为x（0＜x≤2），△BPH的面积为S，则能反映S与x之间的函数关系的图象大致为（ ）
A.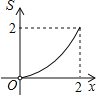
B.
C.
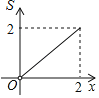D.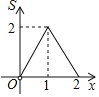
【答案】A
【解析】
过点H作HE⊥BC，垂足为E,易得△BHQ为等腰直角三角形，进而得到HE=
BQ=
，再利用三角形面积公式表示出△BPH的面积，建立S与x之间的函数关系式，即可判断图像.
解：过点H作HE⊥BC，垂足为E,如图，
∵BD是正方形的对角线
∴∠DBC＝45°
∵QH⊥BD
∴△BHQ是等腰直角三角形
又∵HE⊥BQ
∴E为BQ边上的中点，即HE为斜边BQ上的中线
∴HE=BQ=
∴△BPH的面积S＝BPHE＝
＝
∴S与x之间的函数关系是二次函数，且二次函数图象开口方向向上；
因此，选项中只有A选项符合条件．
故选：A．
【题目】定安县定安中学初中部三名学生竞选校学生会主席，他们的笔试成绩和演讲成绩（单位：分）分别用两种方式进行统计，如表和图．
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 |
| 80 | 85 |
（1）请将表和图中的空缺部分补充完整；
（2）图中B同学对应的扇形圆心角为 度；
（3）竞选的最后一个程序是由初中部的300名学生进行投票，三名候选人的得票情况如图（没有弃权票，每名学生只能推荐一人），则A同学得票数为 ，B同学得票数为 ，C同学得票数为 ；
（4）若每票计1分，学校将笔试、演讲、得票三项得分按4：3：3的比例确定个人成绩，请计算三名候选人的最终成绩，并根据成绩判断 当选．（从A、B、C、选择一个填空）
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情，为了引导学生“多读书，读好书”，某校对八年级部分学生的课外阅读量进行了随机调查，整理调查结果发现，学生课外阅读的本数量少的有
本，最多的有
本，并根据调查结果绘制了不完整的图表，如下所示：
本数（本） | 频数（人数） | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
（
）统计图表中的
__________，
__________，
__________．
（
）请将频数分布直方图补充完整．
（
）求所有被调查学生课外阅读的平均本数．
（
）若该校八年级共有
名学生，请你估计该校八年级学生课外阅读
本及以上的人数．
