题目内容
观察按下列规则排成的一列数：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，…（*）
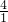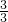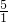（1）在（*）中，从左起第m个数记为F（m），当F（m）=
时，求m的值和这m个数的积
（2）在（*）中，未经约分且分母为2的数记为c，它后面的一个数记为d，是否存在这样的两个数c和d，使cd=2001000，如果存在，求出c和d；如果不存在，说明理由．
解：（1）分组：（），（，），（，，），（，，，），（，，，，），（，…），…，（
，，
，…，
）．
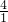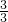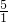当F（m）=时，m=2003003
积为：
，
（2）c为某组倒数第二个数，d为该组最后一个数，
设它们在第n组c=
，d=
，
则
=2001000，
c=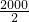
，d=
分析：（1）分数的分子和分母的和为n的一组分数有n-1个，依此求出前面2001组的分数个数，加上2，即可求出m的值，再根据每组的积为1，求出这m个数的积；
（2）先设第n组c=，则d=，根据cd=2001000，列方程求解即可．
点评：本题考查了规律型：数字的变化和一元二次方程的应用．解题关键是得出每组分数对应的分子和分母．
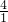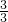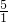），（，），（，，），（，，，），（，，，，），（，…），…，（，，，…，）．当F（m）=
时，m=2003003积为：
，（2）c为某组倒数第二个数，d为该组最后一个数，
设它们在第n组c=
，d=，则
=2001000，c=
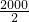，d=分析：（1）分数的分子和分母的和为n的一组分数有n-1个，依此求出前面2001组的分数个数，加上2，即可求出m的值，再根据每组的积为1，求出这m个数的积；
（2）先设第n组c=
，则d=，根据cd=2001000，列方程求解即可．点评：本题考查了规律型：数字的变化和一元二次方程的应用．解题关键是得出每组分数对应的分子和分母．
练习册系列答案
相关题目
时，求m的值和这m个数的积。
时，求m的值和这m个数的积。