题目内容
17.如图,直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则sin∠CBE的值是$\frac{7}{25}$.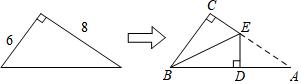
分析 根据翻转变换的性质得到EB=EA,根据勾股定理求出BE、CE,根据正弦的定义计算即可.
解答 解:由折叠的性质可知,EB=EA,
在Rt△BEC中,BE2=CE2+BC2,即BE2=(8-BE)2+62,
解得,BE=$\frac{25}{4}$,
则CE=8-BE=$\frac{7}{4}$,
在Rt△BEC中,sin∠CBE=$\frac{CE}{BE}$=$\frac{7}{25}$,
故答案为:$\frac{7}{25}$.
点评 本题考查的是翻转变换的性质、勾股定理、正弦的概念,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
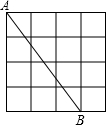 如图,图4×4正方形网格,每个小正方形的边长为l,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
如图,图4×4正方形网格,每个小正方形的边长为l,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上. 如图,在△ABC中,AB=AC,CD=CB,若∠ACD=42°,求∠A的度数.
如图,在△ABC中,AB=AC,CD=CB,若∠ACD=42°,求∠A的度数.