Question

如图，AB是⊙O的直径，BC是⊙O的弦，⊙O的割线PDE垂直AB于点F，交BC于点G，连结PC，∠BAC＝∠BCP，求解下列问题：

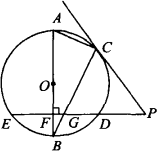
(1)求证：CP是⊙O的切线；

(2)当∠ABC＝30°，BG＝，CG＝时，求以PD、PE的长为两根的一元二次方程；

(3)若(1)的条件不变，当点C在劣弧AD上运动时，应再具备什么条件可使结论BG²＝BF·BO成立？试写出你的猜想，并说明理由．

Answer 1

答案：
解析：

(1)连结OC，证∠OCP＝90°即可; 　　 　　(3)当G为BC中点，OG⊥BC，OG∥AC或∠BOG＝∠BAC…时，结论BG2＝BF·BO成立，要让此结论成立，只要证明△BFG∽△BGO即可，凡是能使△BFG∽△BGO的条件都可以．