Question

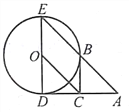
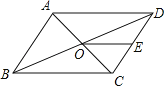
【题目】如图，ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（　　）

A. 15 B. 18 C. 21 D. 24

Answer 1

【答案】A

【解析】

此题涉及的知识点是平行四边形的性质。根据平行四边形的对边相等和对角线互相平分可得，OB=OD，又因为E点是CD的中点，可得OE是△BCD的中位线，可得OE=BC，所以易求△DOE的周长．

解：∵ABCD的周长为36，

∴2（BC+CD）=36，则BC+CD=18．

∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，BD=12，

∴OD=OB=BD=6．

又∵点E是CD的中点，DE=CD，

∴OE是△BCD的中位线，∴OE=BC，

∴△DOE的周长=OD+OE+DE=BD+（BC+CD）=6+9=15，

即△DOE的周长为15．

故选A