题目内容
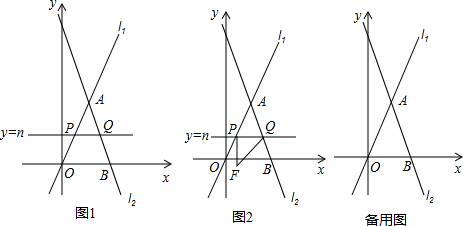
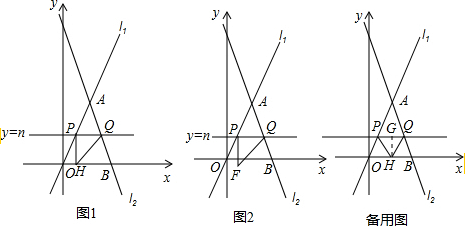
如图1,直线l1:y=2x与直线l2:y=-3x+6相交于点A,直线l2与x轴交于点B,平行于x轴的直线y=n分别交直线l1、直线l2于P、Q两点(点P在Q的左侧)
(1)点A的坐标为______;
(2)如图1,若点P在线段AO上,在x轴上是否存在一点H,使得△PQH为等腰直角三角形,若存在,求出点H的坐标;若不存在,说明理由;
(3)如图2.若以点P为直角顶点,向下作等腰直角△PQF,设△PQF与△AOB重叠部分的面积为S,求S与n的函数关系式;并注明n的取值范围.
 解:(1)∵直线l1:y=2x与直线l2:y=-3x+6相交于点A,
解:(1)∵直线l1:y=2x与直线l2:y=-3x+6相交于点A,∴2x=-3x+6,
解得:x=
 ,
,∴y=
 ,
,∴点A的坐标为(
 ,
, );
);(2)令y=n,则n=2x,
∴
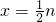 ,
,∴点P(
 ,n),
,n),n=-3x+6,
∴
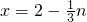 ,
,∴点Q(
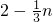 ,n),
,n),∴
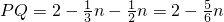 ,
,作PH⊥x轴于H,如图1. 当PH=PQ时△PQH为等腰直角三角形,
∴
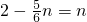 ,
,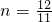 ,
,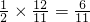 ,
,∴H1(
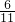 ,0),
,0),作QH⊥x轴于H,如图(备用图),当QH=PQ时△PQH为等腰直角三角形,
同理可得
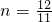
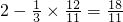 ,
,∴H2(
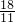 ,0),
,0),当PH=HQ且∠PHQ=90°时,△PQH为等腰直角三角形HG⊥PQ,可得PQ=2HG,
∴
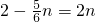 ,
,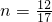 ,
,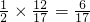 ,
,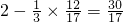 ,
,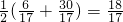 ,
,∴H3(
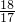 ,0),
,0),∴H点的坐标为(
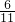 ,0),(
,0),(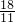 ,0),(
,0),(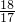 ,0);
,0);(3)当
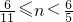 时,
时,∴
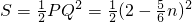 ,
,当
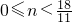 时,
时,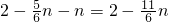 ,
,∴
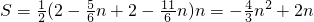 .
.分析:(1)利用两直线相交的性质,使两式相等即可得出答案;
(2)首先表示出PQ的长度,进而得出当PH=HQ且∠PHQ=90°时以及 当PH=PQ时△PQH为等腰直角三角形,分别求出即可;
(3)分别根据当
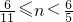 时以及当
时以及当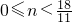 时表示出△PQF与△AOB重叠部分的面积即可.
时表示出△PQF与△AOB重叠部分的面积即可.点评:此题主要考查了一次函数的综合应用以及等腰直角三角形的性质,根据数形结合进行分类讨论是解题关键,注意不要漏解.

练习册系列答案
相关题目
 如图,求直线l1和l2的交点坐标.(要写过程)
如图,求直线l1和l2的交点坐标.(要写过程) 21、如图是四直线L1、L2、L3、L4在坐标平面上的位置,其中有一条直线为方程式y+4=0的图形,求此方程式图形为( )
21、如图是四直线L1、L2、L3、L4在坐标平面上的位置,其中有一条直线为方程式y+4=0的图形,求此方程式图形为( )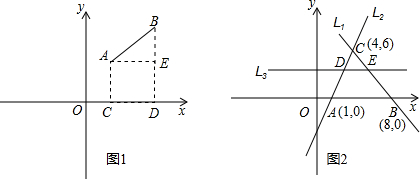
 (2013•贵阳)如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是( )
(2013•贵阳)如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是( )