题目内容
10.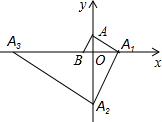 如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为(-31008,0),.
如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为(-31008,0),.
分析 分别写出A1、A2、A3的坐标找到变化规律后写出答案即可.
解答 解:∵A(0,$\sqrt{3}$)、B(-1,0),
∴AB⊥AA1,
∴A1的坐标为:(3,0),
同理可得:A2的坐标为:(0,-3$\sqrt{3}$),A3的坐标为:(-9,0),
…
∵2015÷4=503…3,
∴点A2015横坐标为$-{3}^{\frac{2015+1}{2}}$,即:-31008,
点A2015坐标为(-31008,0),
故答案为:(-31008,0).
点评 本题考查了规律型问题,解题的关键是根据点的坐标的变化得到规律,利用得到的规律解题.

练习册系列答案
相关题目
 如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$.
如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$.
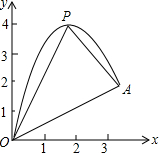 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y=$\frac{1}{2}$x刻画.
如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y=$\frac{1}{2}$x刻画.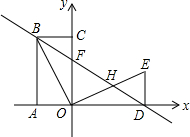 如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是方程x2-6x+8=0的两个根,且OC>BC.
如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是方程x2-6x+8=0的两个根,且OC>BC.