题目内容
 已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.(1)求出A点坐标及直线l2的解析式;
(2)连接BC,求出S△ABC.
分析:(1)根据A点在直线l1上,且横坐标为-1,求出A点的坐标,再根据直线l2过A点,将(-1,1)代入直线l2解析式,即可求出答案;
(2)根据已知得出B点的坐标,再根据l1与y轴交于D点,得出D点和C点的坐标,再根据三角形的面积公式得出S△ABC.
(2)根据已知得出B点的坐标,再根据l1与y轴交于D点,得出D点和C点的坐标,再根据三角形的面积公式得出S△ABC.
解答:解:(1)∵A点在直线l1上,且横坐标为-1,
∴y1=2×(-1)+3=1,即A点的坐标为(-1,1)
又直线l2过A点,将(-1,1)代入直线l2解析式得:1=-k-1,k=-2,
则直线l2的解析式为:y2=-2x-1
(2)l1与x轴交于B点,则B点坐标为(-
,0),l1与y轴交于D点,
则D点坐标为(0,3),l2与y轴交于C点,则C点坐标为(0,-1),
S△ABC=S△BCD-S△ACD=
CD•|xB|-
CD•|xA|=1
∴y1=2×(-1)+3=1,即A点的坐标为(-1,1)
又直线l2过A点,将(-1,1)代入直线l2解析式得:1=-k-1,k=-2,
则直线l2的解析式为:y2=-2x-1
(2)l1与x轴交于B点,则B点坐标为(-
| 3 |
| 2 |
则D点坐标为(0,3),l2与y轴交于C点,则C点坐标为(0,-1),
S△ABC=S△BCD-S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题要注意利用一次函数的特点,列出方程,求出未知数再求得解析式;求三角形的面积时找出高和底边长即可.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=-x-2与坐标轴交于B、D两点,两线的交点为P点,
如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=-x-2与坐标轴交于B、D两点,两线的交点为P点, (2012•卧龙区二模)如图,已知直线l1:y1=x,l2:y2=
(2012•卧龙区二模)如图,已知直线l1:y1=x,l2:y2=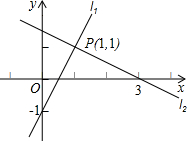 象所提供的信息回答下列问题:
象所提供的信息回答下列问题: 已知直线l1:y1=kx+3与直线l2:y2=-2x交于A点 (-1,m),且直线l1与x轴交于B点,与y轴交于C点.
已知直线l1:y1=kx+3与直线l2:y2=-2x交于A点 (-1,m),且直线l1与x轴交于B点,与y轴交于C点.