题目内容
解不等式:2x2+5x-3>0.
考点:一元二次不等式,因式分解-十字相乘法等,解一元二次方程-公式法,解一元一次不等式组,二次函数与不等式(组)
专题:计算题,数形结合,转化思想
分析:由于初中阶段没有学习解一元二次不等式,不能直接求解,可将该不等式转化为我们熟悉的二次函数,利用二次函数的图象来解,也可将该不等式转化为我们熟悉的不等式组,即可求出该一元二次不等式的解集.
解答:解:方法一:
令y=2x2+5x-3,
当y=0时,2x2+5x-3=0
解得:x1=0.5,x2=-3.
∴抛物线y=2x2+5x-3与x轴的交点为A(0.5,0),B(-3,0),如图所示.
根据图象可得:当x>0.5或x<-3时,y>0即2x2+5x-3>0.
∴不等式2x2+5x-3>0的解集为x>0.5或x<-3.
方法二:
将2x2+5x-3因式分解,得:
2x2+5x-3=(2x-1)(x+3).
∴由2x2+5x-3>0得:
(2x-1)(x+3)>0.
∴Ⅰ:
或Ⅱ;
.
解不等式组Ⅰ得;x>0.5;
解不等式组Ⅱ得;x<-3.
∴不等式2x2+5x-3>0的解集为x>0.5或x<-3.

令y=2x2+5x-3,
当y=0时,2x2+5x-3=0
解得:x1=0.5,x2=-3.
∴抛物线y=2x2+5x-3与x轴的交点为A(0.5,0),B(-3,0),如图所示.
根据图象可得:当x>0.5或x<-3时,y>0即2x2+5x-3>0.
∴不等式2x2+5x-3>0的解集为x>0.5或x<-3.
方法二:
将2x2+5x-3因式分解,得:
2x2+5x-3=(2x-1)(x+3).
∴由2x2+5x-3>0得:
(2x-1)(x+3)>0.
∴Ⅰ:
|
|
解不等式组Ⅰ得;x>0.5;
解不等式组Ⅱ得;x<-3.
∴不等式2x2+5x-3>0的解集为x>0.5或x<-3.
点评:本题考查了一元二次方程的解法、不等式组的解法、因式分解法、二次函数图象的应用等知识,考查了转化的思想以及数形结合的思想,其中将一元二次不等式转化为二次函数或不等式组是解决本题的关键,是考查能力的一道好题.

练习册系列答案
相关题目
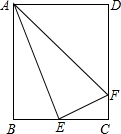 如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设
如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设| AB |
| AD |
(1)△ABE∽△ECF;(2)AE平分∠BAF;(3)当k=1时,△ABE∽△ADF;(4)tan∠EAF=k.
其中结论正确的是( )
| A、(1)(2)(3)(4) |
| B、(1)(3)(4) |
| C、(1)(2) |
| D、(2)(3) |
 某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.