题目内容
6. 如图,点B在线段AC上,且$\frac{BC}{AB}=\frac{AB}{AC}$,设AC=1,则AB的长是( )
如图,点B在线段AC上,且$\frac{BC}{AB}=\frac{AB}{AC}$,设AC=1,则AB的长是( )| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{3+\sqrt{5}}}{2}$ |
分析 根据题意列出一元二次方程,解方程即可.
解答 解:∵$\frac{BC}{AB}=\frac{AB}{AC}$,
∴AB2=1×(1-AB),
∴AB2+AB-1=0,
解得,AB1=$\frac{\sqrt{5}-1}{2}$,AB2=$\frac{-\sqrt{5}-1}{2}$(舍去),
故选:A.
点评 本题考查的是黄金分割的概念以及黄金比值,掌握一元二次方程得到解法、理解黄金分割的概念是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.9的平方根是( )
| A. | ±3 | B. | 3 | C. | 81 | D. | ±81 |
1.方程2x2-x-1=0的两根之和是( )
| A. | -2 | B. | -1 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
15.下列命题的逆命题是真命题的是( )
| A. | 对顶角相等 | B. | 两直线平行,内错角相等 | ||
| C. | 全等三角形的对应角相等 | D. | 第一象限内点的横坐标是正数 |
2.要使a5<a3<a<a2<a4成立,则a的取值范围是( )
| A. | 0<a<1 | B. | a>1 | C. | -1<a<0 | D. | a<-1 |
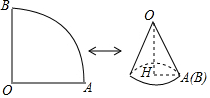 如图,已知扇形AOB的圆心角为90°,面积为16π.
如图,已知扇形AOB的圆心角为90°,面积为16π.