Question

如图，某直升飞机于空中A处观测到其正前方地面控制点C的俯角为30°；若飞机航向不变，继续向前飞行1000米至B处时，观测到其正前方地面控制点C的俯角为45°，问飞机再向前飞行多少米与地面控制点C的距离最近？（结果保留根号）

Answer 1

分析：易得CD=BD，那么利用30°的正切值即可求得BD长，即为飞机再向前飞行多少米与地面控制点C的距离最近．

解答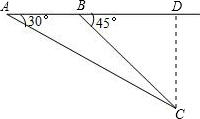：解：做CD⊥AB于点D．
∴∠BDC=90°，
∵∠DBC=45°，
∴BD=CD，
∵∠DAC=30°，
∴tan30°=

CD

AB+DB

=

CD

AB+CD

=

CD

1000+CD

=

3

3

，
解得CD=BD=500

3

+500（米）．
答：飞机再向前飞行（500

3

+500）米与地面控制点C的距离最近．

点评：用到的知识点为：点到直线的最短距离为这点到这条直线的垂线段的长度；借助俯角构造直角三角形并解直角三角形是俯角问题常用的方法．