题目内容
10.已知数轴上两点A,B对应的数分别为-1,3,P为数轴上的动点,其对应的数为x.(1)若点P到A,B两点的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到A,B的距离之和为5?若存在,请求出x的值;若不存在,请说明理由;
(3)当点P以每分钟1个单位长的速度从原点O向左运动时,点A以每分钟5个单位长的速度向左运动,点B以每分钟20个单位长的速度向左运动,问它们同时出发,几分钟后点P到A,B两点的距离相等?
分析 (1)若点P对应的数与-1、3差的绝对值相等,则点P到点A,点B的距离相等.
(2)利用当P在A左侧时,当P在B右侧时,分别得出即可.
(3)利用当P点在AB之间时,此时B到P点距离等于A点到P点距离,以及当P点在AB右侧时,此时A、B重合,求出即可.
解答  解:(1)∵1-(-1)=2,2的绝对值是2,1-3=-2,-2的绝对值是2,
解:(1)∵1-(-1)=2,2的绝对值是2,1-3=-2,-2的绝对值是2,
∴点P对应的数是1.
(2)当P在A左侧时,3-x+(-1-x)=5,
解得:x=-$\frac{3}{2}$;
当P在B右侧时,x-3+x-(-1)=5,
解得:x=$\frac{7}{2}$;
当P在A、B之间时,x不存在;
综上所述,x=-$\frac{3}{2}$或x=$\frac{7}{2}$;
(3))①当B未追上A时,-x+1+5x=3-20x+x,
解得:x=$\frac{2}{23}$;
∴$\frac{2}{23}$分钟时点P到点A、点B的距离相等.
②B追上A时,20x=5x+4,
解得:x=$\frac{4}{15}$,
∴$\frac{4}{15}$分钟时点P到点A、点B的距离相等.
答:当经过$\frac{2}{23}$或$\frac{4}{15}$分钟时,点P到点A,点B的距离相等.
点评 此题主要考查了一元一次方程的应用以及数轴上点的坐标与距离表示方法等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
20. a,b对应如图所示的点,则$\frac{b}{a}$一定是( )
a,b对应如图所示的点,则$\frac{b}{a}$一定是( )
 a,b对应如图所示的点,则$\frac{b}{a}$一定是( )
a,b对应如图所示的点,则$\frac{b}{a}$一定是( )| A. | 正数 | B. | 负数 | C. | 零 | D. | 不能确定 |
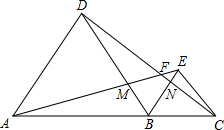 如图,A、B、C三点在同一条直线上,△ABD、△BCE为等边三角形,(等边三角形的三边相等,三个内角都是60°).
如图,A、B、C三点在同一条直线上,△ABD、△BCE为等边三角形,(等边三角形的三边相等,三个内角都是60°).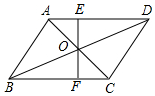 已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是32.
已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是32.