题目内容
已知二次函数
的图象经过点（2，1）。
（1）求二次函数的解析式；
（2）一次函数
的图象与二次函数的图象交于点A（
，
），
B（
，
）两点
①当
时（图①），求证：△AOB为直角三角形；
②试判断当
时（图②），△AOB的形状，并证明；
（3）根据第（2）问，说出一条你能得到的结论（不要求证明）。
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案下列是由四个相同小正方体摆成的立方体图形，它的俯视图是（ ）
| A． B． C． D． |
1． 我州今年参加中考的学生人数大约为
人，对于这个科学记数法表示的近似数，下列说法正确的是（ ）
A．精确到百分位，有3个有效数字 B．精确到百分位，有5个有效数字
C．精确到百位，有3个有效数字 D．精确到百位，有5个有效数字
2． 
如图，将一块三角板的执教顶点放在直尺的一边上，当
时，
（ ）
A．
B．
C．
D．
3． 下列根式中，不能与
合并的是（ ）
A．
B．
C．
D．
某班45名同学某天每人的生活费用统计如下表：
| 生活费（元） | 10 | 15 | 20 | 25 | 30 |
| 学生人数（人） | 4 | 10 | 15 | 10 | 6 |
对于这45名同学这天每人的生活费用，下列说法不正确的是（ ）A．平均数是20 B．众数 C．中位数是20 D．极差是2021世纪教育网版权所有
4． 关于
的一元二次方程
有实数根，则
的取值范围是（ ）
A．
B．
C．且
D．且
5． 将圆心角为
，面积为
的扇形围成一个圆锥的侧面，则所围成圆锥的底面半径为（ ）
A．
B．
C．
D．
6． 在平面直角坐标系中，点
（
，2）关于直线
对称点的坐标是（ ）
A．（，
） B．（3，2） C．（2，） D．（3，）
7． 如图，
内接于
，
，则
的度数为（ ）
A．
B．
C．
D．
8． 以正方形
两条对角线的交点
为坐标原点，建立如图所示的平面直角坐标系，双曲线
经过点
，则正方形的面积是（ ）21·cn·jy·com
A．10 B．11 C．12 D．13
9． 二次函数
（
）的图象如图所示，下列说法：①
；②当
时，
；③若点（
，
）和点（
，
）都在函数的图象上，当
时，
；④
。其中正确的是（ ）21·世纪*教育网
A．① ② ④ B．① ④ C．① ② ③ D．③ ④
第II卷（选择题 共72分）
二、填空题：（共5个小题，每小题4分，共20分）
10．
的平方根是 。
11．已知函数
是正比例函数，则
，
。
12．
小明同学根据全班同学的血型绘制了如图所示的扇形统计图，已知
型血的有20人，则型血的有 人。21教育网
13．分式方程
的解是 。
14．在
中，
、
是
边上的三等分点，连接
、
相交于点，则
。2-1-c-n-j-y
三、解答题：（共2小题，每小题6分，共12分）
15．计算：
；
16．先化简：
，然后从
的范围内选取一个合适的整数作为的值代入求值。
四、解答题：（共3小题，每小题8分，共24分）
17．如图，在楼房
和塔
之间有一棵树
，从楼顶处经过树顶
点恰好看到塔的底部点，且俯角
为
，从楼底
点1米的点处经过树顶点恰好看到塔的顶部
点，且仰角
为
。已知树高
米，求塔的高度（结果保留根号）。
18．如图，在正方形中，
是
上任意一点，连接
，
于，
交于
，探究线段
、
、三者之间的数量关系，并说明理由。
19．2015年5月6日，凉山州政府在邛海“空列”项目考察座谈会上与多方达成初步合作意向，决定共同出资60.8亿元，建设40千米的环邛海空中列车，这将是国内第一条空中列车。据计算，将有24千米的“空列”轨道假设在水上，其余假设在陆地上，并且每千米水上建设费用比陆地建设费用多0.2亿元。 21*cnjy*com
（1）求每千米 “空列”轨道的水上建设费用和陆地建设费用各需多少亿元？
（2）设计在某段“空列”轨道的建设中，每天至少需要运送沙石
，施工方准备租用大、小两种运输车共十辆。已知每辆大车每天运送沙石
，每辆小车每天运送沙石
，大、小车每天每辆租车费用分别是1000元，700元，且要求每天租车的总费用不得超过9300元，问施工方有几种租车方案？那种租车方案费用最低，最低费用是多少？
五、解答题：（共2小题，每小题8分，共16分）
20．有甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0、1、2；乙袋中装有3个完全相同的小球，分别标有数字
、、0；先从甲袋中随机取出一个小球，记录标有的数字为，再从乙袋中随机取出一个小球，记录标有的数字为
，确定点（，）。www.21-cn-jy.com
（1）用树状图或列表法列举点所有可能的坐标；
（2）求点（，）在函数
的图象上的概率 ；
（3）在平面直角坐标系
中，的半径是2，求过点（，）能作的切线的概率；
21．阅读理解：
材料1：一组对边平行，另一组对边不平行的四边形叫梯形。其中平行的两边叫做梯形的底边，不平行的两边叫做梯形的腰。连接梯形两腰中点的线段叫做梯形的中位线。
梯形的中位线具有下列性质：
梯形的中位线平行于两底，并且等于两底和的一半。
如图（1），在梯形中，
。
∵、分别是、
的中点，
∴
，
。
材料2：经过三角形一边的中点与另一边平行的直线必平分第三边。
如图（2），在中，∵是的中点，
，
∴是
的中点。
请你运用所学知识，结合上述材料，解答下列问题：
如图（3），在梯形中，，
于，、分别是、的中点，
。
（1）求证：
；
（2）若
，
，求
的长。
B卷（共30分）
二、填空题：（共2小题，每小题5分，共10分）
22．已知实数、
满足
，
，则
。
23．菱形
在平面直角坐标系中的位置如图所示，顶点（2，0），
，点是对角线
上一个动点， （0，），当
最短时，点的坐标为 。2·1·c·n·j·y
二、解答题：（共2小题，27题8分，28题12分，共20分）
24．如图，的半径为5，点在外，
交于、两点，
交于、两点。
（1）求证：
；（2）若
，
，
，求点到的距离。
25．如图，已知抛物线
的顶点在轴的正半轴上，一次函数
与抛物线交于、两点，与、轴分别交于、两点。
（1）求的值；
（2）求、两点的坐标；
（3）点（
，
）（
）是抛物线上一点，当
得面积是面积的2倍时，求、的值。
的顶点
在
轴的正半轴上，一次函数
与抛物线交于
、
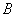两点，与
轴分别交于
、
两点。
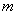的值；
（
，
）（
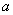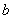）是抛物线上一点，当
得面积是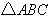
面积的2倍时，求
（
），且
，那么
=_____
时，下列变形正确的为
B.
D.
、
的图象交于B、A两点，则∠OAB大小的变化趋势为
∥
∥
，两条直线与这三条平行线分别交于点
、
、
和
、
、
，已知
，
的值为
．
求证：△ACD ∽ △CBD；