题目内容
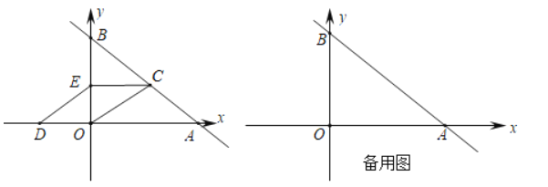
【题目】如图,直线y=-![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=-
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=-![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式;
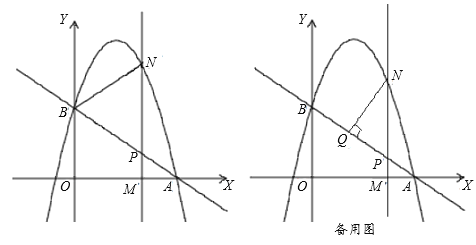
(2)M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若△BPN∽△APM,求点M的坐标;
②过点N作NQ⊥AB于Q,当N点坐标是多少时,NQ取得最大值,最大值是多少?
【答案】(1)B(0,2),![]() ;(2)①M(2.5,0);②
;(2)①M(2.5,0);②![]() 时,NQ有最大值
时,NQ有最大值![]()
【解析】
(1)把A点坐标代入直线解析式可求得c,则可求得B点坐标,由A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)①由M点坐标可表示P、N的坐标,由△BPN∽△APM,得到N点的纵坐标为2,可得到关于m的方程,可求得m的值,即可得到点M的坐标;
②先证出△ABO∽△NPQ,从而得到![]() ,再打AO,AB求出,用含m的式子把PN表示出来,即可得出关于m的二次函数关系式,利用二次函数的性质可得出NQ的最大值.
,再打AO,AB求出,用含m的式子把PN表示出来,即可得出关于m的二次函数关系式,利用二次函数的性质可得出NQ的最大值.
解:(1)∵![]() 与x轴交于点A(3,0),与y轴交于点B,
与x轴交于点A(3,0),与y轴交于点B,
∴可得c=2,
∴B(0,2)
∵抛物线![]() 经过点A,B,
经过点A,B,
∴ 解得
解得
∴抛物线解析式为![]()
(2)①由(1)可知直线解析式为![]()
∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,
∴P![]() , N
, N![]()
∵△BPN∽△APM,且∠BPN=∠APM,
∴∠BNP=∠AMP=90° BN⊥MN,
∴N点的纵坐标为2,
∴![]()
解得m=0(舍去)或m=2.5,
∴M(2.5,0)
②∵MN∥y轴,
∴∠NPQ=∠OBA
又∵∠BOA=∠NQP=90°
∴△ABO∽△NPQ

∴![]()
∴![]()
由(1)及①知AO=3,AB=![]()
PN=![]() -(
-(![]() )=
)=![]()
∴
∴当![]() 时,NQ有最大值
时,NQ有最大值![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题:
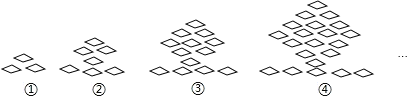
(1)填写下表:
图形序号 | 菱形个数 |
| 3 |
| 7 |
| ______ |
| ______ |
|
|
(2)根据表中规律猜想,图n中菱形的个数![]() 用含n的式子表示,不用说理
用含n的式子表示,不用说理![]() ;
;
(3)是否存在一个图形恰好由91个菱形组成?若存在,求出图形的序号;若不存在,说明理由.