题目内容
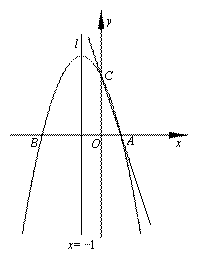
如图,已知直线 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线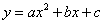 经过点A和点C,对称轴为直线l:
经过点A和点C,对称轴为直线l: ,该抛物线与x轴的另一个交点为B.
,该抛物线与x轴的另一个交点为B.
(1)求此抛物线的解析式;
(2)点P在直线l上,求出使△PAC的周长最小的点P的坐标;
(3)点M在此抛物线上,点N在y轴上,以A、B、M、N为顶点的四边形能否为平行四边形?若能,直接写出所有满足要求的点M的坐标;若不能,请说明理由.
 |
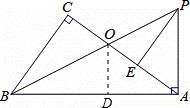
(1)证明:∵∠C=90°,∠BAP=90°
∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,
又∵∠CBO=∠ABP,
∴∠BOC=∠ABP,
∵∠BOC=∠AOP,
∴∠AOP=∠ABP,
∴AP=AO;
(2)证明:如图,过点O作OD⊥AB于D,
∵∠CBO=∠ABP,
∴CO=DO,
∵AE=OC,
∴AE=OD,
∵∠AOD+∠OAD=90°,∠PAE+∠OAD=90°,
∴∠AOD=∠PAE,
在△AOD和△PAE中,
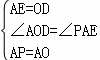 ,
,
∴△AOD≌△PAE(SAS),
∴∠AEP=∠ADO=90°
∴PE⊥AO;
(3)解:设AE=OC=3k,
∵AE=AC,∴AC=8k,
∴OE=AC﹣AE﹣OC=2k,
∴OA=OE+AE=5k.
由(1)可知,AP=AO=5k.
如图,过点O作OD⊥AB于点D,
∵∠CBO=∠ABP,∴OD=OC=3k.
在Rt△AOD中,AD=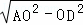 =
= =4k.
=4k.
∴BD=AB﹣AD=10﹣4k.
∵OD∥AP,
∴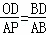 ,即
,即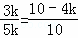
∵AB=10,PE=AD,
∴PE=AD=4K,BD=AB﹣AD=10﹣4k,
由∠CBO=∠ABP,根据轴对称BC=BD=10﹣4k,
∵∠BOC=∠EOP,∠C=∠PEO=90°,
∴△BCO∽△PEO,
∴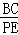 =
=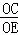 ,即
,即 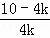 =
=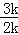 ,
,
解得k=1.
∴BD=10﹣4k=6,OD=3k=3,
在Rt△BDO中,由勾股定理得:
BO=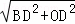 =
=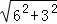 =3
=3 .
.

计算sin245°+cos30°•tan60°,其结果是( )
|
| A. | 2 | B. | 1 | C. |
| D. |
|
关于x的一元二次方程x2+2(m﹣1)x+m2=0的两个实数根分别为x1,x2,且x1+x2>0,x1x2>0,则m的取值范围是( )
|
| A. | m≤ | B. | m≤ | C. | m<1 | D. | m<1且m≠0 |
 ,则最后输出的结果是( )
,则最后输出的结果是( )




 B.
B. 
 D.
D. 
 -
-  = 2.
= 2.