Question

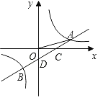
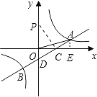
【题目】如图，一次函数的图象与反比例函数的图象交于，两点，与轴交于点，与轴交于点，已知，，点的坐标为．

求反比例函数的解析式；

求一次函数的解析式；

在轴上存在一点，使得与相似，请你求出点的坐标．

Answer 1

【答案】 ； 点坐标为．

【解析】

（1）中，因为OA＝，tan∠AOC＝，则可过A作AE垂直x轴，垂足为E，利用三角函数和勾股定理即可求出AE＝1，OE＝3，从而可知A（3，1），又因点A在反比例函数y＝的图象上，由此可求出开k＝3，从而求出反比例函数的解析式；

（2）中，因为一次函数y＝ax＋b的图象与反比例函数y＝的图象交于A，B两点，点B的坐标为（m，2）．所以3＝2x．即m＝，B（，2）．然后把点A、B的坐标代入一次函数的解析式，得到关于a、b的方程组，解之即可求出a、b的值，最终写出一次函数的解析式；

（3）因为在y轴上存在一点P，使得△PDC与△ODC相似，而∠PDC和∠ODC是公共角，所以有△PDC∽△CDO，，，而点C、D分别是一次函数y＝x1的图象与x轴、y轴的交点，因此有C（，0）、D（0，1）．OC＝，OD＝1，DC＝．进而可求出PD＝，OP＝．写出点P的坐标．

过作垂直轴，垂足为，

∵，

∴，

∵，，

∴，，

∴点的坐标为．

∵点在双曲线上，

∴，

∴．

∴双曲线的解析式为；

∵点在双曲线上，

∴，

∴．

∴点的坐标为．

∴，∴，

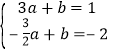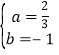∴一次函数的解析式为；

过点作，交轴于点，

∵，两点在直线上，

∴，的坐标分别是：，．

即：，，

∴．

∵，

∴，

∴，

又，

∴点坐标为．