题目内容
 图中是抛物线形拱桥,水面在AB时,拱顶离水面4米,水面宽为8米.
图中是抛物线形拱桥,水面在AB时,拱顶离水面4米,水面宽为8米.
(1)若以M为坐标原点建立平面直角坐标系,求出抛物线的解析式;
(2)若现水位上升1米,水面宽度减少多少?(结果保留根号)
 解:(1)如图,建立直角坐标,
解:(1)如图,建立直角坐标,可设这条抛物线为y=ax2,
把点(4,-4)代入,得
-4=a×42,a=-
 ,
,∴y=-
 x2,
x2,(2)当y=-3时,-3=-
 x2,x=2
x2,x=2 ,
,∴水面上升1m,水面宽度减少(8-4
 )m.
)m.分析:(1)首先建立直角坐标系,设抛物线为y=ax2,把点(4,-4)代入求出解析式可解.
(2)根据当y=-3时,求出x的值,即可得出水面宽度减少的长度.
点评:此题主要考查了点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
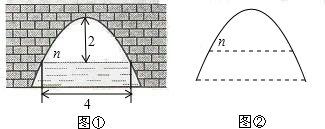
 图中是抛物线形拱桥,水面在AB时,拱顶离水面4米,水面宽为8米.
图中是抛物线形拱桥,水面在AB时,拱顶离水面4米,水面宽为8米. 图中是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?
图中是抛物线形拱桥,当水面宽为4米时,拱顶距离水面2米;当水面高度下降1米时,水面宽度为多少米?
