题目内容
6. 已知:如图,PM⊥BD于BD中点M,PN⊥AD于AD中点N,PM=PN,试说明:OB=OA.
已知:如图,PM⊥BD于BD中点M,PN⊥AD于AD中点N,PM=PN,试说明:OB=OA.
分析 证明Rt△PMD≌Rt△PND,得到∠BDO=∠ADO和DB=DA,证明△BOD≌△AOD,证明结论.
解答 证明:在Rt△PMD和Rt△PND中,
$\left\{\begin{array}{l}{PM=PN}\\{PD=PD}\end{array}\right.$,
∴Rt△PMD≌Rt△PND,
∴∠BDO=∠ADO,DM=DN,又DM=$\frac{1}{2}$BD,DN=$\frac{1}{2}$DA,
∴DB=DA,
在△BOD和△AOD中,
$\left\{\begin{array}{l}{DB=DA}\\{∠BDO=∠ADO}\\{DO=DO}\end{array}\right.$,
∴△BOD≌△AOD,
∴OB=OA.
点评 本题考查的是三角形全等的判定和性质,灵活运用三角形全等的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
17.下列为真命题的是( )
| A. | 相等的角是对顶角 | B. | 直角三角形都相似 | ||
| C. | 两直线平行,同旁内角相等 | D. | 两点之间线段最短 |
15.甲楼高度为7m,乙楼比甲楼低2m,乙楼的高度为( )
| A. | -7m | B. | -2m | C. | 2m | D. | 5m |
 已知(如图所示)A(3,2),B(3,4),C(-4,-2),D(2,-2),
已知(如图所示)A(3,2),B(3,4),C(-4,-2),D(2,-2),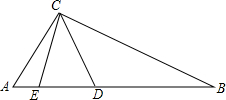 马明和王群在解这样一道题:“如图,在△ABC中,∠ACB=90°,点D、E在边AB上,AD=AC,BE=BC.求∠DCE的度数.”他们经过商量后,结论不一致,马明说:“∠DCE的值与∠B有关,只有告诉∠B的度数才能求出∠DCE的度数.”王群说:“∠DCE的度数是一个定值,与∠B的度数无关.”他们谁说的正确?请说明理由.
马明和王群在解这样一道题:“如图,在△ABC中,∠ACB=90°,点D、E在边AB上,AD=AC,BE=BC.求∠DCE的度数.”他们经过商量后,结论不一致,马明说:“∠DCE的值与∠B有关,只有告诉∠B的度数才能求出∠DCE的度数.”王群说:“∠DCE的度数是一个定值,与∠B的度数无关.”他们谁说的正确?请说明理由. 如图,在平行四边形ABCD中,点M、N是对角线AC上的点,且AM=CN,DE=BF,求证:四边形MFNE是平行四边形.
如图,在平行四边形ABCD中,点M、N是对角线AC上的点,且AM=CN,DE=BF,求证:四边形MFNE是平行四边形.