题目内容
O是△ABC的内心,若∠AOC=160°,则∠ABC的度数是________.
140°
分析:在△AOC中,利用三角形内角和定理即可求得∠OAC和∠OCA的和,然后根据内心的定义可以得到∠BAC+∠BCA=2(∠OAC+∠OCA),然后利用三角形的内角和定理即可求解.
解答: 解:∵O是△ABC的内心,
解:∵O是△ABC的内心,
∴∠OAC= ∠BAC,∠OCA=
∠BAC,∠OCA= ∠BCA,
∠BCA,
∴∠BAC+∠BCA=2(∠OAC+∠OCA),
∵△OAC中,∠OAC+∠OCA=180°-∠AOC=180°-160°=20°,
∴∠BAC+∠BCA=40°,
∴∠BAC=180°-(∠BAC+∠BCA)=180°-40°=140°.
故答案是:140°.
点评:本题考查了内心的性质,以及三角形内角和定理,正确得到∠BAC+∠BCA=2(∠OAC+∠OCA)是关键.
分析:在△AOC中,利用三角形内角和定理即可求得∠OAC和∠OCA的和,然后根据内心的定义可以得到∠BAC+∠BCA=2(∠OAC+∠OCA),然后利用三角形的内角和定理即可求解.
解答:
 解:∵O是△ABC的内心,
解:∵O是△ABC的内心,∴∠OAC=
 ∠BAC,∠OCA=
∠BAC,∠OCA= ∠BCA,
∠BCA,∴∠BAC+∠BCA=2(∠OAC+∠OCA),
∵△OAC中,∠OAC+∠OCA=180°-∠AOC=180°-160°=20°,
∴∠BAC+∠BCA=40°,
∴∠BAC=180°-(∠BAC+∠BCA)=180°-40°=140°.
故答案是:140°.
点评:本题考查了内心的性质,以及三角形内角和定理,正确得到∠BAC+∠BCA=2(∠OAC+∠OCA)是关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
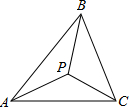 如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB的度数为( )
如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB的度数为( )| A、150° | B、120° | C、90° | D、60° |
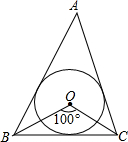 如图所示,O是△ABC的内心,∠BOC=100°,则∠BAC=
如图所示,O是△ABC的内心,∠BOC=100°,则∠BAC=
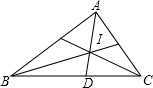 如图,I是△ABC的内心,∠A=40°,则∠CIB=
如图,I是△ABC的内心,∠A=40°,则∠CIB= 如图,AB是圆O的直径,AB=10,点C是圆O上一动点(与A,B不重合),∠ACB的平分线交圆O于D.
如图,AB是圆O的直径,AB=10,点C是圆O上一动点(与A,B不重合),∠ACB的平分线交圆O于D.