Question

已知：如图，一次函数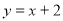的图象与反比例函数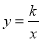的图象交于A、B两点，且点A的坐标为（1，m）．

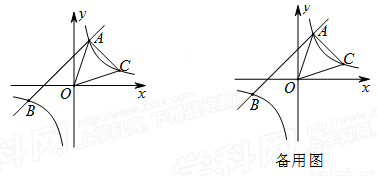
（1）求反比例函数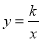的表达式；

（2）点C（n，1）在反比例函数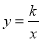的图象上，求△AOC的面积；

（3）在x轴上找出点P，使△ABP是以AB为斜边的直角三角形，请直接写出所有符合条件的点P的坐标．

Answer 1

（1）；（2）4；（3）P1（，0），P2（，0）．

【解析】

试题分析：（1）把（1，m）依次代入一次函数的解析式，得到A的坐标，再把A的坐标代入反比例函数解析式，即可得到反比例函数的解析式；

（2）由反比例函数得到C的坐标，从而求出△AOC的面积；

（3）以AB为直径作⊙M与x轴相交于P，则MP=AB，由两点间距离公式求出P的坐标即可．

试题解析：（1）∵点A（1，m）在一次函数的图象上，∴ m=3，∴ 点A的坐标为（1，3），∵点A（1，3）在反比例函数的图象上，∴ k =3，∴反比例函数的表达式为；

（2）∵点C（n，1）在反比例函数的图象上，∴ n=3，∴ C（3，1），过A作AD⊥x轴于D，过C作CE⊥x轴于E，∴，∵，∴，∴；

（3）以AB为直径作⊙M与x轴相交于P，设P（x，0），∵，解得：，或，∴B（－3，－1），∵A(1，3)，∴P（－1，1），AB=，∵MP为直角三角形BPA斜边的中线，∴MP=AB， ∴，解得：，∴所有符合条件的点P的坐标：P1（，0），P2（，0）．

考点：反比例函数综合题．