题目内容
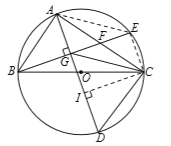
【题目】如图,![]() 内接于
内接于![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,弦
上一点,弦![]() 交
交![]() 于点
于点![]() ,弦
,弦![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() .
.
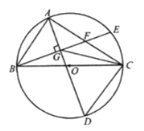
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)证法一:连接![]() ,利用圆周角定理得到
,利用圆周角定理得到![]() ,从而证明
,从而证明![]() ,然后利用同弧所对的圆周角相等及三角形外角的性质得到
,然后利用同弧所对的圆周角相等及三角形外角的性质得到![]() ,从而使问题得解;证法二:连接
,从而使问题得解;证法二:连接![]() ,
,![]() ,由圆周角定理得到
,由圆周角定理得到![]() ,从而判定
,从而判定![]() ,得到
,得到![]() ,然后利用圆内接四边形对角互补可得
,然后利用圆内接四边形对角互补可得![]() ,从而求得
,从而求得![]() ,使问题得解;
,使问题得解;
(2)首先利用勾股定理和三角形面积求得AG的长,解法一:过点![]() 作
作![]() 于点
于点![]() ,利用勾股定理求GH,CH,CD的长;解法二:过点
,利用勾股定理求GH,CH,CD的长;解法二:过点![]() 作
作![]() 于点
于点![]() ,利用AA定理判定
,利用AA定理判定![]() ,然后根据相似三角形的性质列比例式求解.
,然后根据相似三角形的性质列比例式求解.
(1)证法一:连接![]() .
.
∵![]() 为
为![]() 的直径,∴
的直径,∴![]() ,
,
∴![]()
∵![]() ,∴
,∴![]()
∴![]()
∴![]() .
.
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() .
.
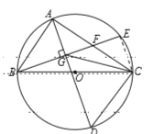
证法二:连接![]() ,
,![]() .
.
∵![]() 为
为![]() 的直径,∴
的直径,∴![]()
∵![]()
∴![]()
∴![]() ,
,
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵四边形![]() 内接于
内接于![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]() .
.
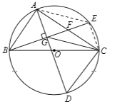
(2)解:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
根据勾股定理得![]() .
.
连接![]() ,
,![]()
∵![]() 为
为![]() 的直径,
的直径,
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() .
.
在![]() 中,
中,![]()
![]() ,
,
∴![]()
解法一:过点![]() 作
作![]() 于点
于点![]()
∴![]()
在![]() 中,
中,![]() ,
,![]()
∴![]()
在![]() 中,
中,![]()
∴![]()
在![]() 中,
中,![]()
∴![]()
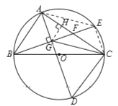
解法二:过点![]() 作
作![]() 于点
于点![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴四边形![]() 为矩形
为矩形
∴![]() .
.
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]()
∴![]() .
.
∵![]() ,
,![]()
∴![]()
∴![]() 即
即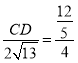
∴![]()

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】先锋中学数学课题组为了了解初中学生阅读数学教科书的现状,随机抽取某校部分初中学生进行调查,调查结果分为“重视”、“一般”、“不重视”、“说不清楚”四种情况(依次用A、B、C、D表示),依据相关数据绘制成以下不完整的统计表和统计图,请根据图表中的信息解答下列问题:
类别 | 频数 | 频率 |
重视 | a | 0.25 |
一般 | 60 | 0.3 |
不重视 | b | c |
说不清楚 | 10 | 0.05 |
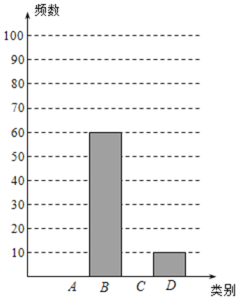
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有2000名学生,请估计该校“不重视阅读数学教科书”的学生人数.