题目内容
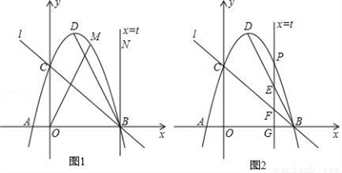
在平面直角坐标系中,抛物线y=ax2﹣2ax+a+4(a<0)经过点A(﹣1,0),且与x轴正半轴交于点B,与y轴交于点C,点D是顶点.
(1)填空:a=_____;顶点D的坐标为______;直线BC的函数表达式为:_________.
(2)直线x=t与x轴相交于一点.
①当t=3时得到直线BN(如图1),点M是直线BC上方抛物线上的一点.
若∠COM=∠DBN,求出此时点M的坐标.
②当1<t<3时(如图2),直线x=t与抛物线、BD、BC及x轴分别相交于点P、E、F、G,3试证明线段PE、EF、FG总能组成等腰三角形;如果此等腰三角形底角的余弦值为0.6,求此时t的值.
 全能闯关100分系列答案
全能闯关100分系列答案(6分) 某仓库原有某种货物库存270千克,现规定运入为正,运出为负,一天中
七次出入如下(单位:千克)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-30 | +80 | -20 | +100 | -96 | +35 | -24 |
求这一天最终的库存量;
若货物装卸费用为每千克0.2元,问这一天需装卸费多少元?
某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?


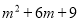 =________________.
=________________.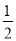 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
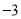 和2为根的一元二次方程: 。
和2为根的一元二次方程: 。
 平分对角
平分对角