题目内容
6.已知方程x2+px+q=0的两个根分别是3和-5,则x2+px+q可分解为( )| A. | (x+3)(x+5) | B. | (x-3)(x-5) | C. | (x-3)(x+5) | D. | (x+3)(x-5) |
分析 根据因式分解法解一元二次方程的方法,当方程x2+px+q=0的两个根分别是3和-5时,则原方程转化为x-3=0或x+5=0,于是得到x2+px+q=(x-3)(x+5).
解答 解:∵方程x2+px+q=0的两个根分别是3和-5,
∴原方程为(x-3)(x+5)=0,
所以x2+px+q可分解为(x-3)(x+5).
故选C.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
14.60的$\frac{2}{5}$相当于80的( )
| A. | $\frac{3}{8}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
11.在-$\frac{π}{3}$,$\sqrt{16}$,$\frac{\sqrt{2}}{2}$,0.3030030003,-$\frac{22}{7}$,3.14中,有理数有几个( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
15.下列说法正确的是( )
| A. | -a一定是负数 | B. | $\frac{2011}{3}$是有理数 | ||
| C. | 2$\sqrt{2}$是有理数 | D. | 平方等于自身的数只有1 |
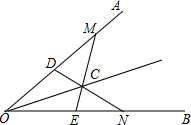 如图,小明用三角尺画∠AOB的平分线,他先在∠AOB两边OA,OB上分别取OM=ON,OD=OE,然后,连接DN和EM,相交于点C,再作射线OC,此时他认为OC就是∠AOB的平分线,你认为他的做法正确吗?请说明理由.
如图,小明用三角尺画∠AOB的平分线,他先在∠AOB两边OA,OB上分别取OM=ON,OD=OE,然后,连接DN和EM,相交于点C,再作射线OC,此时他认为OC就是∠AOB的平分线,你认为他的做法正确吗?请说明理由.