题目内容
12.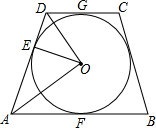 在四边形ABCD中,AB∥CD,⊙O分别与AD、AB、CD相切于E、F、G,连接OA、OD、OE.求证:∠AOE=$\frac{1}{2}$∠ADC.
在四边形ABCD中,AB∥CD,⊙O分别与AD、AB、CD相切于E、F、G,连接OA、OD、OE.求证:∠AOE=$\frac{1}{2}$∠ADC.
分析 连接OG、OF.由DC∥AB可知∠CDA+∠DAB=180°,然后证明△DEO≌DOG,从而得到∠EDO=$\frac{1}{2}$∠ADC,同理:∠DAO=$\frac{1}{2}$∠DAF,于是可证明∠AOD=90°,然后利用切线的性质可证明∠OEA=90°,接下来再证明∠AOE=∠ADO,故此可得到∠AOE=$\frac{1}{2}$∠ADC.
解答 证明:如图连接OG、OF.
∵DC∥AB,
∴∠CDA+∠DAB=180°.
∵DE、DG是圆0的切线,
∴DE=DG.
在△DEO和DOG中$\left\{\begin{array}{l}{DE=DG}\\{OE=OG}\\{OD=OD}\end{array}\right.$,
∴△DEO≌DOG.
∴∠EDO=∠GDO.
∴∠EDO=$\frac{1}{2}$∠ADC.
同理:∠DAO=$\frac{1}{2}$∠DAF.
∴∠EAO+∠EDO=$\frac{1}{2}$(∠DAF+∠ADG)=90°.
∴∠AOD=90°.
∵AD是圆O的切线,
∴OE⊥AD.
∴∠OEA=90°.
∵∠EAO=∠DAO,∠OEA=∠AOD,
∴∠AOE=∠ADO.
∴∠AOE=$\frac{1}{2}$∠ADC.
点评 本题主要考查的是切线的性质、全等三角形的性质和判定、平行线的性质的应用,证得∠AOD=90°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知点D,E分别在AC、AB上,∠B=∠C.除对顶角外.图中还有哪些角分别相等?证明你的结论.
如图,已知点D,E分别在AC、AB上,∠B=∠C.除对顶角外.图中还有哪些角分别相等?证明你的结论. 如图,直线AB,CD,EF相交于O
如图,直线AB,CD,EF相交于O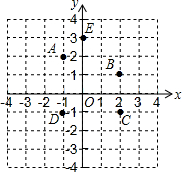 写出如图中的点A、B、C、D、E、F的坐标,观察这些点的坐标,回答下列问题.
写出如图中的点A、B、C、D、E、F的坐标,观察这些点的坐标,回答下列问题. 如图,圆内接正五边形ABCDE中,对角线AC和BE相交于圆内的点P,求证:△APB为等腰三角形.
如图,圆内接正五边形ABCDE中,对角线AC和BE相交于圆内的点P,求证:△APB为等腰三角形.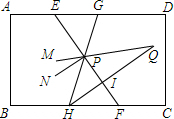 如图,AD∥BC,EF、HG交于点P,HI平分∠GHF,PM平分∠EPH,HI交PM的反向延长线于Q,PN∥HI,则:①若∠EGP=∠GEP,则PM∥AD;②∠GEP=2∠MPN;③∠EPN=2∠Q,其中正确的是②.
如图,AD∥BC,EF、HG交于点P,HI平分∠GHF,PM平分∠EPH,HI交PM的反向延长线于Q,PN∥HI,则:①若∠EGP=∠GEP,则PM∥AD;②∠GEP=2∠MPN;③∠EPN=2∠Q,其中正确的是②.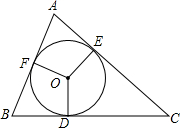 △ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,且AB=11cm,BC=16cm,CA=15cm,求AF、BD、CE的长?
△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,且AB=11cm,BC=16cm,CA=15cm,求AF、BD、CE的长?