题目内容
已知(-1,y1),(-2,y2),(2,y3)是抛物线y=-x2-4x+m上的点,则( )
| A、y3<y1<y2 |
| B、y1<y3<y2 |
| C、y1<y2<y3 |
| D、y2<y3<y1 |
考点:二次函数图象上点的坐标特征
专题:
分析:求出抛物线的对称轴为直线x=-2,然后根据二次函数的增减性和对称性解答即可.
解答:解:抛物线的对称轴为直线x=-
=-2,
∵a=-1<0,
∴x=-2时,函数值最大,
又∵-1到-2的距离比2到-2的距离小,
∴y3<y1<y2.
故选A.
| -4 |
| 2×(-1) |
∵a=-1<0,
∴x=-2时,函数值最大,
又∵-1到-2的距离比2到-2的距离小,
∴y3<y1<y2.
故选A.
点评:本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性和对称性,求出对称轴是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
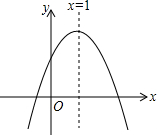 二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论:①b2-4ac>0;②a>0;③b>0;④c>0;⑤4a+2b+c<0,则其中结论正确的个数是( )
二次函数y=ax2+bx+c(a≠0)图象如图所示,现有下列结论:①b2-4ac>0;②a>0;③b>0;④c>0;⑤4a+2b+c<0,则其中结论正确的个数是( )| A、2个 | B、3个 | C、4个 | D、5个 |
若x2-2(k-1)x+4是完全平方式,则k的值为( )
| A、±1 | B、±3 |
| C、-1或3 | D、1或-32 |
 尺规作图(不要求写出作法,但要保留作图痕迹)
尺规作图(不要求写出作法,但要保留作图痕迹) 如图,在△ABC中,D、E分别是AB、AC上的点,△ADE∽△ABC,∠ADE=∠B,∠AED=∠C,AD=4,AE=3,EB=5,求CD的长.
如图,在△ABC中,D、E分别是AB、AC上的点,△ADE∽△ABC,∠ADE=∠B,∠AED=∠C,AD=4,AE=3,EB=5,求CD的长.