Question

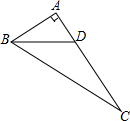
如图所示，在Rt△ABC中，AB=BC=4，∠ABC=90°，点P是△ABC的外角∠BCN的角平分线上一个动点，点P′是点P关于直线BC的对称点，连结PP′交BC于点M，BP′交AC于D，连结BP、AP′、CP′．
（1）若四边形BPCP′为菱形，求BM的长；
（2）若△BMP′∽△ABC，求BM的长；
（3）若△ABD为等腰三角形，求△ABD的面积．

Answer 1

【答案】分析：（1）由菱形的性质可知，点M为BC的中点，所以BM可求；
（2）△ABC为等腰直角三角形，若△BMP′∽△ABC，则△BMP′必为等腰直角三角形．证明△BMP′、△BMP、△BPP′均为等腰直角三角形，则BP=BP′；证明△BCP为等腰三角形，BP=BC，从而BP′=BC=4，进而求出BM的长度；
（3）△ABD为等腰三角形，有3种情形，需要分类讨论计算．
解答：解：（1）∵四边形BPCP′为菱形，而菱形的对角线互相垂直平分，
∴点M为BC的中点，
∴BM=BC=×4=2．

（2）△ABC为等腰直角三角形，若△BMP′∽△ABC，
则△BMP′必为等腰直角三角形，BM=MP′．
由对称轴可知，MP=MP′，PP′⊥BC，则△BMP为等腰直角三角形，
∴△BPP′为等腰直角三角形，BP′=BP．
∵∠CBP=45°，∠BCP=（180°-45°）=67.5°，
∴∠BPC=180°-∠CBP-∠BCP=180°-45°-67.5°=67.5°，
∴∠BPC=∠BCP，
∴BP=BC=4，
∴BP′=4．
在等腰直角三角形BMP′中，斜边BP′=4，
∴BM=BP′=．

（3）△ABD为等腰三角形，有3种情形：
①若AD=BD，如题图②所示．
此时△ABD为等腰直角三角形，斜边AB=4，
∴S_△ABD=AD•BD=××=4；
②若AD=AB，如下图所示：

过点D作DE⊥AB于点E，则△ADE为等腰直角三角形，
∴DE=AD=AB=
∴S_△ABD=AB•DE=×4×=；
③若AB=BD，则点D与点C重合，可知此时点P、点P′、点M均与点C重合，
∴S_△ABD=S_△ABC=AB•BC=×4×4=8．
点评：本题是几何综合题，考查了相似三角形的性质、等腰直角三角形、等腰三角形、菱形、勾股定理等知识点，难度不大．第（3）问考查了分类讨论的数学思想，是本题的难点．